
科目: 来源: 题型:
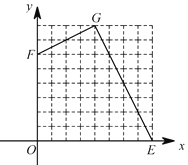
【题目】如图,在平面直角坐标系 ![]() 中,
中,![]() ,
,![]() .
.
①当 ![]() 时,则
时,则![]() ______;
______;
②在图中的网格区域内找一点![]() ,使
,使![]() ,且四边形
,且四边形![]() 被过
被过![]() 点的一条直线分割成两部分后,可以拼成一个正方形,则
点的一条直线分割成两部分后,可以拼成一个正方形,则![]() 点坐标为_______.
点坐标为_______.
查看答案和解析>>
科目: 来源: 题型:
【题目】推理填空:
如图,![]() ,
,![]() ,将说明
,将说明![]() 成立的理由填写完整.
成立的理由填写完整.

解:因为![]() (已知),
(已知),
所以![]() (________________)
(________________)
又因为![]() (已知),
(已知),
所以![]() (等量代换),
(等量代换),
所以________________(同位角相等,两直线平行),
所以![]() (________________________________)
(________________________________)
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料,并解决后面的问题.
材料:一般地,![]() 个相同的因数
个相同的因数![]() 相乘:
相乘:![]() 个
个![]() 记为
记为![]() ,如
,如![]() ,此时,3叫做以2为底8的对数,记为
,此时,3叫做以2为底8的对数,记为![]() (即
(即![]() ).
).
一般地,若![]() (
(![]() 且
且![]() ,
,![]() ),则
),则![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记为
的对数,记为![]() (即
(即![]() ).如
).如![]() ,则4叫做以3为底81的对数,记为
,则4叫做以3为底81的对数,记为![]() (即
(即![]() ).
).
问题:(1)计算以下各对数的值:![]() ________,
________,![]() ________,
________,![]() ________.
________.
(2)观察(1)中三数4、16、64之间满足怎样的关系式?![]() 、
、![]() 、
、![]() 之间又满足怎样的关系式?______________________________________________________________________________
之间又满足怎样的关系式?______________________________________________________________________________
(3)由(2)的结果,你能归纳出一个一般性的结论吗?
![]() ____________________(
____________________(![]() 且
且![]() ,
,![]() ,
,![]() )
)
(4)根据幂的运算法则:![]() 以及对数的含义证明(3)中结论.
以及对数的含义证明(3)中结论.
查看答案和解析>>
科目: 来源: 题型:
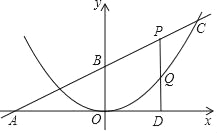
【题目】如图,直线y=kx+b与坐标轴交于A,B两点,其中点B的坐标为(0,4),tan∠BAO=![]() ,一条抛物线的顶点为坐标原点,且与直线y=kx+b交于点C(m,8),点P为线段BC上一动点(不与点B,点C重合),PD⊥x轴于点D,交抛物线于点Q.
,一条抛物线的顶点为坐标原点,且与直线y=kx+b交于点C(m,8),点P为线段BC上一动点(不与点B,点C重合),PD⊥x轴于点D,交抛物线于点Q.
(1)求直线和抛物线的函数关系式;
(2)设点P的横坐标为t,线段PQ的长度为d,求出d与t之间的函数关系式,并求出d的最大值;
(3)是否存在点P的位置,使得以点P,D,B为顶点的三角形是等腰三角形?如果存在,直接写出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
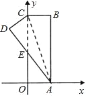
【题目】如图,在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点E的坐标_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】(本题满分10分)已知四边形ABCD是矩形,对角线AC和BD相交于点P,若在矩形的上方加一个△DEA,且使DE∥AC,AE∥BD.
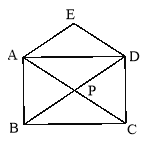
(1)求证:四边形DEAP是菱形;
(2)若AE=CD,求∠DPC的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是ts(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:四边形AEFD是平行四边形;
(2)当t为何值时,△DEF为直角三角形?请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该商场两次共购进这种运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润不低于20%,那么每套售价至少是多少元?
查看答案和解析>>
科目: 来源: 题型:
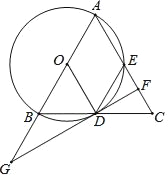
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O交BC,AC于D,E两点,过点D作⊙O的切线,交AC于点F,交AB的延长线于点G.
(1)求证:EF=CF;
(2)若cos∠ABC=![]() ,AB=10,求线段AF的长.
,AB=10,求线段AF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com