
科目: 来源: 题型:
【题目】如图,顶点为P(4,-4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M、N关于点P对称,连接AN、ON.
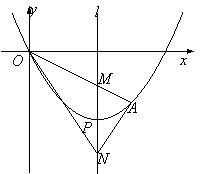
(1)求该二次函数的关系式;
(2)若点A的坐标是(6,-3),求△ANO的面积;
(3)当点A在对称轴l右侧的二次函数图象上运动时,请解答下面问题:
①证明:∠ANM=∠ONM;
②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标;如果不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两人两次同时在一家粮店购买大米,两次大米的价格分别为每千克a元和b元(a≠b).甲每次买100千克大米,乙每次买100元大米.
(1)用含a、b的代数式表示:甲两次购买大米共需付款 元,乙两次共购买 千克大米.若甲两次购买大米的平均单价为每千克Q1元,乙两次购买大米的平均单价为每千克Q2元.则:Q1= ;Q2= .
(2)若规定谁两次购粮的平均价格低,谁购粮的方式就更合理,请你判断比较甲、乙两人的购粮方式,哪一个更合理,并说明你的理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】为方便市民通行,某广场计划对坡角为30°,坡长为60 米的斜坡AB进行改造,在斜坡中点D 处挖去部分坡体(阴影表示),修建一个平行于水平线CA 的平台DE 和一条新的斜坡BE.

(1)若修建的斜坡BE 的坡角为36°,则平台DE的长约为多少米?
(2)在距离坡角A点27米远的G处是商场主楼,小明在D点测得主楼顶部H 的仰角为30°,那么主楼GH高约为多少米?
(结果取整数,参考数据:sin 36°=0.6,cos 36°=0.8,tan 36°=0.7,![]() =1.7)
=1.7)
查看答案和解析>>
科目: 来源: 题型:
【题目】将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀.

(1)这部分男生有多少人?其中成绩合格的有多少人?
(2)这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,张三打算在院落种上蔬菜.已知院落为东西长为32米,南北宽为20米的长方形,为了行走方便,要修筑同样宽度的三条小路,东西两条,南北一条,余下的部分种上各类蔬菜.若每条小路的宽均为1米.
(1)求蔬菜的种植面积;
(2)若每平方米的每季蔬菜的值为3元,成本为1元,这个院落每季的产值是多少?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形ABCD中,AD=2![]() ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为___.
,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为___.
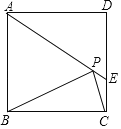
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示:
(1)直接写出点A的坐标,点A关于x轴的对称点B的坐标,点B关于y轴的对称点C的坐标.
(2)画出将线段BC向右平移2个单位,再向上平移4个单位后的线段B′C′,并直接写出B′的坐标.
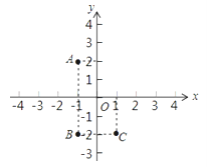
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
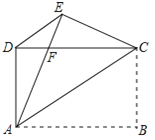
(1)求证:△DEC≌△EDA;
(2)求DF的值;
查看答案和解析>>
科目: 来源: 题型:
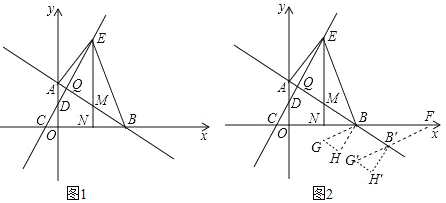
【题目】如图1,在平面直角坐标系中,直线AB与y轴交于点![]() ,与x轴交于点B,
,与x轴交于点B,![]() ,直线CD与y轴交于点D,与x轴交于点
,直线CD与y轴交于点D,与x轴交于点![]() ,
,![]() ,直线AB与直线CD交于点Q,E为直线CD上一动点,过点E作x轴的垂线,交直线AB于点M,交x轴于点N,连接AE、BE.
,直线AB与直线CD交于点Q,E为直线CD上一动点,过点E作x轴的垂线,交直线AB于点M,交x轴于点N,连接AE、BE.
![]() 求直线AB、CD的解析式及点Q的坐标;
求直线AB、CD的解析式及点Q的坐标;
![]() 当E点运动到Q点的右侧,且
当E点运动到Q点的右侧,且![]() 的面积为
的面积为![]() 时,在y轴上有一动点P,直线AB上有一动点R,当
时,在y轴上有一动点P,直线AB上有一动点R,当![]() 的周长最小时,求点P的坐标及
的周长最小时,求点P的坐标及![]() 周长的最小值.
周长的最小值.
![]() 在
在![]() 问的条件下,如图2将
问的条件下,如图2将![]() 绕着点B逆时针旋转
绕着点B逆时针旋转![]() 得到
得到![]() ,使点M与点G重合,点N与点H重合,再将
,使点M与点G重合,点N与点H重合,再将![]() 沿着直线AB平移,记平移中的
沿着直线AB平移,记平移中的![]() 为
为![]() ,在平移过程中,设直线
,在平移过程中,设直线![]() 与x轴交于点F,是否存在这样的点F,使得
与x轴交于点F,是否存在这样的点F,使得![]() 为等腰三角形?若存在,求出此时点F的坐标;若不存在,说明理由
为等腰三角形?若存在,求出此时点F的坐标;若不存在,说明理由
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在梯形ABCD中,AB∥CD,∠B=90°,AB=2,CD=1,BC=m,P为线段BC上的一动点,且和B、C不重合,连接PA,过P作PE⊥PA交CD所在直线于E.设BP=x,CE=y.

(1)求y与x的函数关系式;
(2)若点P在线段BC上运动时,点E总在线段CD上,求m的取值范围;
(3)如图2,若m=4,将△PEC沿PE翻折至△PEG位置,∠BAG=90°,求BP长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com