
科目: 来源: 题型:
【题目】如图,M,N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞,工程人员为计算工程量,必须测量M、N两点之间的直线距离.选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米,AN=1.8千米,AB=54米,BC=45米,AC=30米,求M、N两点之间的直线距离.

【答案】M、N两点之间的直线距离为1500米.
【解析】试题分析:先根据相似三角形的判定得出△ABC∽△AMN,再利用相似三角形的性质解答即可.
试题解析:在△ABC与△AMN中, ![]() ,
, ![]() =
=![]() ,∴
,∴![]() ,又∵∠A=∠A,
,又∵∠A=∠A,
∴△ABC∽△AMN,∴![]() ,即
,即![]() ,
,
解得:MN=1500米,
答:M、N两点之间的直线距离是1500米;
考点:相似三角形的应用.
【题型】解答题
【结束】
23
【题目】如图,在△ADC中,点B是边DC上的一点,∠DAB=∠C, ![]() .若△ADC的面积为18cm,求△ABC的面积.
.若△ADC的面积为18cm,求△ABC的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数y=(m﹣2)xm2+m-4 +2x﹣1是一个二次函数,求该二次函数的解析式.
【答案】y=﹣5x2+2x﹣1
【解析】试题分析:根据二次函数的定义得到m2+m﹣4=2且m﹣2≠0,由此求得m的值,进而得到该二次函数的解析式.
试题解析:依题意得:m2+m﹣4=2且m﹣2≠0. 即(m﹣2)(m+3)=0且m﹣2≠0,
解得m=﹣3,
则该二次函数的解析式为y=﹣5x2+2x﹣1
【题型】解答题
【结束】
21
【题目】如图,在ABCD中,EF∥AB,FG∥ED,DE:DA=2:5,EF=4,求线段CG的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】把一张对面互相平行的纸条折成如图所示,EF是折痕,若∠EFB=32°,则下列结论不正确的有( ).
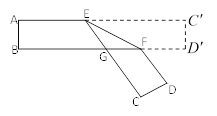
A.![]() B.∠AEC=148°C.∠BGE=64°D.∠BFD=116°
B.∠AEC=148°C.∠BGE=64°D.∠BFD=116°
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知△ABC三个顶点的坐标分别是A(-2,3),B(-3,-1),C(-1,1)
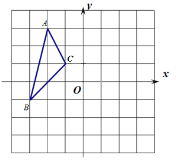
(1)画出△ABC绕点O逆时针旋转90°后的△A1B1C1,并写出点A1的坐标;
(2)画出△ABC绕点O逆时针旋转180°后的△A2B2C2,并写出点A2的坐标;
(3)直接回答:∠AOB与∠A2OB2有什么关系?
【答案】(1)作图见解析,(-4,-2);(2)作图见解析,(2,-3);(3)相等.
【解析】
试题分析:(1)根据旋转的性质作图,写出点的坐标;
根据旋转的性质作图,写出点的坐标;
(3)根据旋转的性质得出结论.
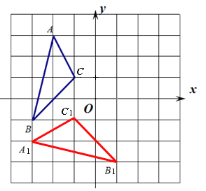
试题解析:(1)作图如下,点A1的坐标(-4,-2).
(2)作图如下,点A2的坐标(2,-3).
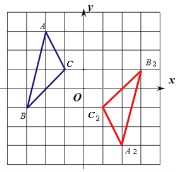
(3)相等.
考点:1.旋转作图;2.旋转的性质.
【题型】解答题
【结束】
20
【题目】已知函数y=(m﹣2)xm2+m-4 +2x﹣1是一个二次函数,求该二次函数的解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】一次函数![]() 和
和![]() 的图象如图所示,且
的图象如图所示,且![]() ,
,![]() .
.
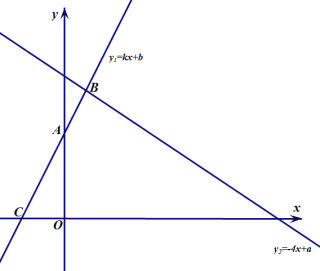
(1)由图可知,不等式![]() 的解集是______;
的解集是______;
(2)若不等式![]() 的解集是
的解集是![]() .
.
①点![]() 的坐标为______.
的坐标为______.
②![]() 的值为_______.
的值为_______.
查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数y=x2+(2m+1)x+(m2﹣1)有最小值﹣2,则m=________.
【答案】![]()
【解析】试题解析:∵二次函数有最小值﹣2,
∴y=﹣![]() ,
,
解得:m=![]() .
.
【题型】填空题
【结束】
19
【题目】如图,已知△ABC三个顶点的坐标分别是A(-2,3),B(-3,-1),C(-1,1)

(1)画出△ABC绕点O逆时针旋转90°后的△A1B1C1,并写出点A1的坐标;
(2)画出△ABC绕点O逆时针旋转180°后的△A2B2C2,并写出点A2的坐标;
(3)直接回答:∠AOB与∠A2OB2有什么关系?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,完成下列推理过程:
如图所示,点E在![]() 外部,点D在BC边上,DE交AC于F,若
外部,点D在BC边上,DE交AC于F,若![]() ,
,![]() ,
,
求证:![]() .
.

证明:∵![]() (已知),
(已知),
![]() (________________),
(________________),
∴![]() (________________),
(________________),
又∵![]() ,
,
∴________![]() ________
________![]() (________),
(________),
即![]() ,
,
在![]() 和
和![]() 中
中
![]() (已证)
(已证)
∵![]() (已知)
(已知)
![]() (已证)
(已证)
∴![]() (________).
(________).
∴![]() (________________)
(________________)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图:已知点A、B是反比例函数y=﹣![]() 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.

【答案】![]()
【解析】过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,过点A作AF⊥BE轴于点F,如图所示.

∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
又∵AD⊥y轴,BE⊥y轴,
∴∠ACD+∠CAD=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,∠BCE=∠CAD.
在△ACD和△CBE中,由 ,
,
∴△ACD≌△CBE(ASA).
设点B的坐标为(m,﹣![]() )(m<0),则E(0,﹣
)(m<0),则E(0,﹣![]() ),点D(0,3﹣m),点A(﹣
),点D(0,3﹣m),点A(﹣![]() ﹣3,3﹣m),
﹣3,3﹣m),
∵点A(﹣![]() ﹣3,3﹣m)在反比例函数y=﹣
﹣3,3﹣m)在反比例函数y=﹣![]() 上,
上,
 ,解得:m=﹣3,m=2(舍去).
,解得:m=﹣3,m=2(舍去).
∴点A的坐标为(﹣1,6),点B的坐标为(﹣3,2),点F的坐标为(﹣1,2),
∴BF=2,AF=4,
![]()
故答案为:2![]() .
.
【点睛】
过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,过点A作AF⊥BE轴于点F,根据角的计算得出“∠ACD=∠CBE,∠BCE=∠CAD”,由此证出△ACD≌△CBE;再设点B的坐标为(m,﹣![]() ),由三角形全等找出点A的坐标,将点A的坐标代入到反比例函数解析式中求出m的值,将m的值代入A,B点坐标即可得出点A,B的坐标,并结合点A,B的坐标求出点F的坐标,利用勾股定理即可得出结论.
),由三角形全等找出点A的坐标,将点A的坐标代入到反比例函数解析式中求出m的值,将m的值代入A,B点坐标即可得出点A,B的坐标,并结合点A,B的坐标求出点F的坐标,利用勾股定理即可得出结论.
【题型】填空题
【结束】
18
【题目】二次函数y=x2+(2m+1)x+(m2﹣1)有最小值﹣2,则m=________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图:已知点A、B是反比例函数y=﹣![]() 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com