
科目: 来源: 题型:
【题目】如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,CB1=CB,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过100,最少经过( )次操作.
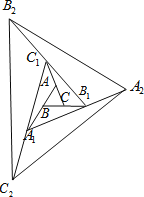
A.3B.4C.5D.6
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂生产一种合金薄板(其厚度忽略不计)这些薄板的形状均为正方形,边长(单位:cm)在5~50之间,每张薄板的成本价(单位:元)与它的面积(单位:cm2)成正比例,每张薄板的出厂价(单位:元)由基础价和浮动价两部分组成,(即出厂价=基础价+浮动价)其中基础价与薄板的大小无关,是固定不变的,浮动价与薄板的边长x成正比例,在营销过程中得到了表格中的数据,已知出厂一张边长为40cm的薄板,获得利润是26元.(利润=出厂价-成本价)
薄板的边长(cm) | 20 | 30 |
出厂价(元/张) | 50 | 70 |
(1)求一张薄板的出厂价y与边长x之间满足的函数关系式;
(2)求一张薄板的利润p与边长x之间的函数关系式;
(3)若一张薄板的利润是34元,且成本最低,此时薄板的边长为多少?当薄板的边长为多少时,所获利润最大,求出这个最大值。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为F,线段FD,AB的延长线相交于点G.

(1)求证:DF是⊙O的切线;
(2)若CF=2,DF=2![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】等腰Rt△ACB,∠ACB=90°,AC=BC,点A、C分别在x轴、y轴的正半轴上.

(1)如图1,求证:∠BCO=∠CAO
(2)如图2,若OA=5,OC=2,求B点的坐标
(3)如图3,点C(0,3),Q、A两点均在x轴上,且S△CQA=18.分别以AC、CQ为腰在第一、第二象限作等腰Rt△CAN、等腰Rt△QCM,连接MN交y轴于P点,OP的长度是否发生改变?若不变,求出OP的值;若变化,求OP的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠B=∠C,AB=10 cm,BC=8 cm,D为AB的中点,点P在线段上以3 cm/s的速度由点B向点C运动,同时,点Q在线段CA上以相同速度由点C向点A运动,一个点到达终点后另一个点也停止运动.当△BPD与△CQP全等时,求点P运动的时间.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠BAC=∠BCA,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌ Rt△CBF;
(2)求证:AE⊥CF;
(3)若∠CAE=30°,求∠ACF度数.

查看答案和解析>>
科目: 来源: 题型:
【题目】某体育场看台的坡面AB与地面的夹角是37°,看台最高点B到地面的垂直距离BC为2.4米,看台正前方有一垂直于地面的旗杆DE,在B点用测角仪测得旗杆的最高点E的仰角为33°,已知测角仪BF的高度为1.2米,看台最低点A与旗杆底端D之间的距离为15米(C,A,D在同一条直线上).
(1)求看台最低点A到最高点B的坡面距离AB;
(2)一面红旗挂在旗杆上,固定红旗的上下两个挂钩G、H之间的距离为1.2米,下端挂钩H与地面的距离为1米,要求用30秒的时间将红旗升到旗杆的顶端,求红旗升起的平均速度(计算结果保留两位小数)(sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,sin33°≈0.54,cos33°≈0.84,tan33°≈0.65)

查看答案和解析>>
科目: 来源: 题型:
【题目】随着教育信息化的发展,学生的学习方式日益增多. 教师为了指导学生有幸效利用网络进行学习,对学生进行了随机问卷调查(问卷调查表如图所示),并用调查结果绘制了图1、图2两幅统计图(均不完整),请根据统计图解答以下问题:


(1)本次接受问卷调查的学生共有 人;在扇形统计图中“D”选项所占的百分比为 ;
(2)扇形统计图中,“B”选项所对应扇形圆心角为 度;
(3)请补全条形统计图;
(4)若该校共有1200名学生,请你估计该校学生课外利用网络学习的时间在“A”选项的有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,CA⊥AB,垂足为 A,AB=24,AC=12,射线 BM⊥AB,垂足为 B, 一动点 E 从 A点出发以 3 厘米/秒沿射线 AN 运动,点 D 为射线 BM 上一动点, 随着 E 点运动而运动,且始终保持 ED=CB,当点 E 经过______秒时,△DEB 与△BCA 全等.
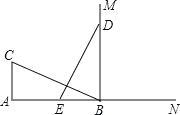
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com