
科目: 来源: 题型:
【题目】如图:在4×4的正方形(每个小正方形的边长均为1)网格中,以A为顶点,其他三个顶点都在格点(网格的交点)上,且面积为2的平行四边形共有多少个?( )

A.12B.16C.24D.25
查看答案和解析>>
科目: 来源: 题型:
【题目】近年来,青少年中的近视眼和肥胖案例日趋增多,人们普遍意识到健康的身体是学习的保障,所以体育活动越来越受重视.某商店分两次购进跳绳和足球两种商品进行销售,每次购进同一种商品的进价相同,具体情况如下表所示.
购进数量(件) | 购进所需费用(元) | ||
跳绳 | 足球 | ||
第一次 | 30 | 40 | 3800 |
第二次 | 40 | 30 | 3200 |
(1)跳绳和足球两种商品每件的进价分别是多少元?
(2)商店计划用5300元的资金进行第三次进货,共购进跳绳和足球两种商品100件,其中要求足球的数量不少于跳绳的数量,有哪几种进货方案?
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,将抛物线C1:y=x2绕点(1,0)旋转180°后,得到抛物线C2,定义抛物线C1和C2上位于﹣2≤x≤2范围内的部分为图象C3.若一次函数y=kx+k﹣1(k>0)的图象与图象C3有两个交点,则k的范围是:__.
查看答案和解析>>
科目: 来源: 题型:
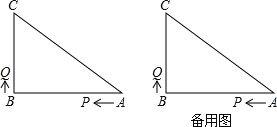
【题目】如图,在△ABC中,∠B=90°,AB=8厘米,BC=6厘米,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动速度为1厘米/秒,点Q从点B开始沿B→C→A方向运动速度为2厘米/秒,若它们同时出发,设出发的时间为t秒.
(1)求出发2秒后,PQ的长;
(2)点Q在CA边上运动时,当△BCQ成为等腰三角形时,求点Q的运动时间.
查看答案和解析>>
科目: 来源: 题型:
【题目】我市举行“第十七届中小学生书法大赛”作品比赛,已知每幅参赛作品成绩记为![]() ,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
分数段 | 频数 | 百分比 |
| 38 | 0.38 |
|
| 0.32 |
|
|
|
| 10 | 0.1 |
合计 | 100 | 1 |
书法作品比赛成绩频数直方图

根据上述信息,解答下列问题:
(1)请你把表中空白处的数据填写完整.
(2)请补全书法作品比赛成绩频数直方图.
(3)若80分(含80分)以上的书法作品将被评为等级奖,试估计全市获得等级的幅数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 的坐标为(0,4),线段
的坐标为(0,4),线段![]() 的位置如图所示,其中点
的位置如图所示,其中点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),点
),点![]() 的坐标为(3,
的坐标为(3,![]() ).
).

(1)将线段![]() 平移得到线段
平移得到线段![]() ,其中点
,其中点![]() 的对应点为
的对应点为![]() ,点
,点![]() 的对应点为点
的对应点为点![]() .
.
①点![]() 平移到点
平移到点![]() 的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
②点![]() 的坐标为 .
的坐标为 .
(2)在(1)的条件下,若点![]() 的坐标为(4,0),连接
的坐标为(4,0),连接![]() ,画出图形并求
,画出图形并求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与X轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:
①4a﹣2b+c<0;②2a﹣b<0;③a+c<1;④b2+8a>4ac,
其中正确的有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
查看答案和解析>>
科目: 来源: 题型:
【题目】认真阅读下面的材料,完成有关问题.
材料:在学习绝对值时,老师教过我们绝对值的几何含义,如![]() 表示
表示![]() 、
、![]() 在数轴上对应的两点之间的距离;
在数轴上对应的两点之间的距离;![]() ,所以
,所以![]() 表示
表示![]() 、
、![]() 在数轴上对应的两点之间的距离;
在数轴上对应的两点之间的距离;![]() ,所以
,所以![]() 表示
表示![]() 在数轴上对应的点到原点的距离.
在数轴上对应的点到原点的距离.
一般地,点![]() 、点
、点![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() 、
、![]() ,那么点
,那么点![]() 、点
、点![]() 之间的距离可表示为
之间的距离可表示为![]() .
.
(1)点![]() 、
、![]() 、
、![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() 、
、![]() 、
、![]() ,那么点
,那么点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到点
到点![]() 的距离之和可表示为__________(用含绝对值的式子表示).
的距离之和可表示为__________(用含绝对值的式子表示).
(2)利用数轴探究:
①满足![]() 的
的![]() 的取值范围是__________.
的取值范围是__________.
②满足![]() 的
的![]() 的所有值是__________.
的所有值是__________.
③设![]() ,当
,当![]() 的值取在不小于
的值取在不小于![]() 且不大于
且不大于![]() 的范围时,
的范围时,![]() 的值是不变的,而且是
的值是不变的,而且是![]() 的最小值,这个最小值是_____.
的最小值,这个最小值是_____.
(3)拓展:
①![]() 的最小值为__________.
的最小值为__________.
②![]() 的最小值为__________.
的最小值为__________.
③![]() 的最小值为__________,此时
的最小值为__________,此时![]() 的取值范围为__________.
的取值范围为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com