
科目: 来源: 题型:
【题目】如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B.

(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足kx+b≥(x-2)2+m的x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
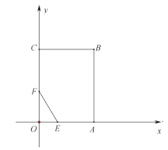
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别落在
分别落在![]() 轴、
轴、![]() 轴正半轴上,点
轴正半轴上,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,且
上,且![]() ,已知
,已知![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)点![]() 关于点
关于点![]() 的对称点为点
的对称点为点![]() ,点
,点![]() 从
从![]() 点出发,以每秒1个单位的速度沿射线
点出发,以每秒1个单位的速度沿射线![]() 运动,设
运动,设![]() 点的运动时间为
点的运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() ;
;
(3)在(2)的条件下,点![]() 为平面内一点,点
为平面内一点,点![]() 在线段
在线段![]() 上运动时,作
上运动时,作![]() 的平分线交
的平分线交![]() 轴于点
轴于点![]() ,
,![]() 为何值时,四边形
为何值时,四边形![]() 为矩形?并求此时点
为矩形?并求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利50元.为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多售出2件.设每件商品降价x元.据此规律,请回答:
(1)商场日销售量增加______件,每件商品盈利______.元(用含![]() 的代数式表示);
的代数式表示);
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到1428元?
查看答案和解析>>
科目: 来源: 题型:
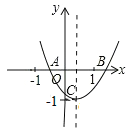
【题目】已知:二次函数y=ax2+bx+c的图象如图所示,OA=OC,则由抛物线的特征写出如下含有a、b、c三个字母的等式或不等式:①![]() =-1;②ac+b+1=0;③abc>0;④a-b+c>0.正确的序号是______________.
=-1;②ac+b+1=0;③abc>0;④a-b+c>0.正确的序号是______________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象过点M(﹣2, ![]() ),顶点坐标为N(﹣1,
),顶点坐标为N(﹣1, ![]() ),且与x轴交于A、B两点,与y轴交于C点.
),且与x轴交于A、B两点,与y轴交于C点.
(1)求抛物线的解析式;
(2)点P为抛物线对称轴上的动点,当△PBC为等腰三角形时,求点P的坐标;
(3)在直线AC上是否存在一点Q,使△QBM的周长最小?若存在,求出Q点坐标;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】张翔上午7:30出发,从学校骑自行车去县城,路程全长20km,中途因道路施工步行一段路.他步行的平均速度是5km/h
(1)若张翔骑车的平均速度是15km/h,当天上午9:00到达县城,则他骑车与步行各用多少时间?
(2)若张翔必须在当天上午9:00之前赶到县城,他的步行平均速度不变,则他骑车的平均速度应在什么范围内?
查看答案和解析>>
科目: 来源: 题型:
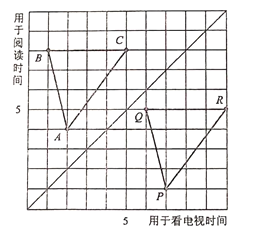
【题目】图中,点A,B,C,P,Q,R显示了6名学生平均每周用于阅读课外书的时间和用于看电视的时间(单位:h)
(1)用有序数对表示图中点A,B,C,P,Q,R
(2)图中方格纸的对角线的左上方的点有什么共同的特点?它右下方的点呢?
(3)三角形ABC的图形经过怎样的变换后得到三角形PQR的图形?其中点A对应点P,点B对应点Q,点C对应点R
查看答案和解析>>
科目: 来源: 题型:
【题目】圣母大学计算机系的史戈宇教授带一家人去旅行,途中汽车被劫走报警911,警察无作为,汽车上安装的MS系统,可以提示汽车与手机APP间的直线距离。史教授用“贪心算法”把被盗车辆位置确定在了图中灰色的区域里,这是一个以暴乱和枪击闻名的地区。当史教授开车从E向A的方向行驶时,汽车与手机APP间的直线距离逐渐变小,从A向F的方向行驶时,汽车与手机APP问的直线距离逐渐变大.当史教授开车从F向B的方向行驶时,汽车与手机APP间的直线距离逐渐变小,从B向G的方向行驶时,汽车与手机APP间的直线距离逐渐变大. 史教授再次报警后,警察根据史教授确定的被盗汽车的位置,很快找到了被盗汽车根据你学的数学知识,在图中,画出被盗汽车的位置.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图1,四边形ABCD是平行四边形,E,F是对角线AC上的两点,AE=CF.
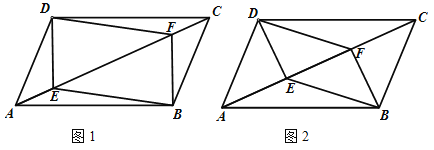
(1)求证:四边形DEBF是平行四边形;
(2)如果AE=EF=FC,请直接写出图中2所有面积等于四边形DEBF的面积的三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com