
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.

(1)求证:四边形ADCF是菱形;
(3)若AC=6,AB=8,求菱形ADCF的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】一家商铺进行维修,若请甲、乙两名工人同时施工,![]() 天可以完成,共需支付两人工资
天可以完成,共需支付两人工资![]() 元,若先请甲工人单独做
元,若先请甲工人单独做![]() 天,再请乙工人单独做
天,再请乙工人单独做![]() 天也可完成,共需付给两人工资
天也可完成,共需付给两人工资![]() 元
元
![]() 甲、乙工人单独工作一天,商铺应分别支付多少工资?
甲、乙工人单独工作一天,商铺应分别支付多少工资?
![]() 单独请哪名工人完成,商铺支付维修费用较少?
单独请哪名工人完成,商铺支付维修费用较少?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知y﹣3与2x﹣1成正比例,且当x=1时,y=6.
(1)求y与x之间的函数解析式.
(2)当x=2时,求y的值.
(3)若点A(x1,y1),B(x2,y2)都在该函数的图象上,且y1>y2,试判断x1,x2的大小关系.
查看答案和解析>>
科目: 来源: 题型:
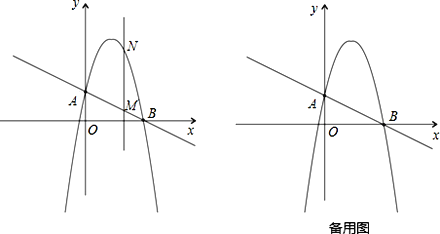
【题目】如图,一次函数![]() 分别交y轴、x 轴于A、B两点,抛物线
分别交y轴、x 轴于A、B两点,抛物线![]() 过A、B两点.
过A、B两点.
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于点M,交这个抛物线于点N.求当t 取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC,BD相交于点O,AC=12,BD=16,E为AD中点,点P在x轴上移动.若△POE为等腰三角形,请写出所有符合要求的点P的坐标 .

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
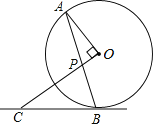
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为3,OP=1,求BC的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,Rt△ABO的顶点A是双曲线![]() 与直线
与直线![]() 在第二象限的交点,AB⊥
在第二象限的交点,AB⊥![]() 轴于点B且S△ABO=
轴于点B且S△ABO=![]() .
.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A,C的坐标;
(3)求△AOC的面积.

查看答案和解析>>
科目: 来源: 题型:
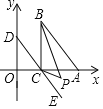
【题目】如图,在直角坐标系中,三角形![]() 两顶点的坐标为
两顶点的坐标为![]() ,
,![]() ,点
,点![]() 是
是![]() 轴上一动点(不与点
轴上一动点(不与点![]() 重合),过点
重合),过点![]() 作
作![]() ,
,![]() 分别平分
分别平分![]() .
.
(1)当点![]() 在点
在点![]() 左边,三角形
左边,三角形![]() 的面积为6时,求点
的面积为6时,求点![]() 的坐标.
的坐标.
(2)当![]() 轴时,求
轴时,求![]() 的度数.
的度数.
(3)当点![]() 在点
在点![]() 右边时,写出
右边时,写出![]() 与
与![]() 的数量关系(不用说理).
的数量关系(不用说理).
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙在一段长2000米的直线公路上进行跑步练习,起跑时甲在起点,乙在甲的前面,若甲、乙同时起跑至甲到达终点的过程中,甲乙之间的距离y(米)与 时间x(秒)之间的函数关系如图所示.有下列说法:
①甲的速度为5米/秒;②100秒时甲追上乙;③经过50秒时甲乙相距50米;④甲到终点时,乙距离终点300米.其中正确的说法有( )

A. 4个 B. 3个
C. 2个 D. 1个
查看答案和解析>>
科目: 来源: 题型:
【题目】完全平方公式:(a±b)2=a2±2ab+b2适当的变形,可以解决很多的数学问题.
例如:若a+b=3,ab=1,求a2+b2的值.
解:因为a+b=3,ab=1
所以(a+b)2=9,2ab=2
所以a2+b2+2ab=9,2ab=2
得a2+b2=7
根据上面的解题思路与方法,解决下列问题:
(1)若(7﹣x)(x﹣4)=1,求(7﹣x)2+(x﹣4)2的值;
(2)如图,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=5,两正方形的面积和S1+S2=17,求图中阴影部分面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com