
科目: 来源: 题型:
【题目】数轴上A,B,C三个点对应的数分别为a,b,x,且A,B到﹣1所对应的点的距离都等于7,点B在点A的右侧,
(1)请在数轴上表示点A,B位置,a= ,b= ;
(2)请用含x的代数式表示CB= ;
(3)若点C在点B的左侧,且CB=8,点A以每秒2个单位长度的速度沿数轴向右运动,当AC=2AB且点A在B的左侧时,求点A移动的时间.
查看答案和解析>>
科目: 来源: 题型:
【题目】利用图象法求方程的解,体现了数形结合的方法,它是将方程的解看成两个函数图象交点的横坐标.若关于x的方程x2+a﹣![]() =0(a>0)只有一个整数解,则a的值等于 .
=0(a>0)只有一个整数解,则a的值等于 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系 ;
(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
(3)在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )

A.  B.
B.  C.
C.  D.
D. 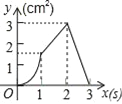
查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数![]() ,自变量x与函数y的对应值如下表:
,自变量x与函数y的对应值如下表:
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | … |
y | … | 4 | 0 | ﹣2 | ﹣2 | 0 | 4 | … |
则下列说法正确的是( )
A. 抛物线的开口向下 B. 当x>![]() 时,y随x的增大而增大
时,y随x的增大而增大
C. 二次函数的最小值是![]() D. 抛物线的对称轴是
D. 抛物线的对称轴是![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】新个税法于2018年1月1日起施行,2018年10月1日起施行最新“起征点:5000元”和税率,《中华共和国个人所得税》中的个人所得税税率如下:
级数 | 全月应纳税所得额 | 税率(%) |
1 | 不超过3000元的部分 | 3 |
2 | 超过3000元至12000元的部分 | 10 |
3 | 超过12000元至25000元的部分 | 20 |
其中“全月应纳税所得额”是指从工资、薪金收入中减去5000元后的金额。(本题只讨论上表内容)
(1)若某一月份扣除税后拿了8000,他交了多少税?
(2)若某一月份纳税额为m元(m>0),他的税前收入是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在数轴上有A,B,C三个点,请回答:

(1)如果将A点向右移动4个单位长度,表示什么数?
(2)如果将点C向左移动3个单位长度,三个点中哪个点表示的数最大?是多少?
(3)如果点A、点B同时向右运动,点A的速度是2个单位/秒,点B的速度是1个单位/秒,问经过多长时间两点重合?
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)定义“*”是一种运算符号,规定![]() ,则
,则![]() =________.
=________.
(2)宾馆重新装修后,准备在大厅的主楼梯上铺设一种红地毯,已知这种地毯每平方米售价40元,主楼梯道宽2米,其侧面如图所示,则买地毯至少需要___________________ 元.

查看答案和解析>>
科目: 来源: 题型:
【题目】问题:探究函数y=|x|-1的性质.
小凡同学根据学习函数的经验,对函数y=|x|-1的图象与性质进行了探究.下面是小凡的探究过程,请补充完整:
(1)在函数y=|x|-1中,自变量x的取值范围是______________;
(2)下表是y与x的几组对应值.
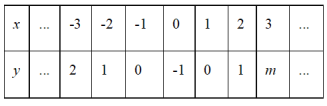
①m=_________;
②若A(n,9),B(10,9)为该函数图象上不同的两点,则n=__________;
(3)如下图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并根据描出的点,画出该函数的图象;
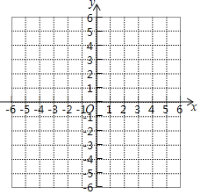
(4)结合函数图象,解决问题:
①该函数有______(填“最大值”或“最小值”);并写出这个值为______;
②观察函数y=|x|-1的图象,写出该图象的两条性质.
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于A(4,0),B(6,0)两点,与
轴交于A(4,0),B(6,0)两点,与![]() 轴交于点C(0,3).
轴交于点C(0,3).
(1)求抛物线的解析式;
(2)点P从点O出发,以每秒2个单位长度的速度向点B运动,同时点E也从点O出发,以每秒1个单位长度的速度向点C运动,设点P的运动时间为t秒(0<t<3).
①过点E作x轴的平行线,与BC相交于点D(如图所示),当t为何值时,△PDE的面积最大,并求出这个最大值;
②当t =2时,抛物线的对称轴上是否存在点F,使△EFP为直角三角形?若存在,请你求出点F的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com