
科目: 来源: 题型:
【题目】周长相等的正三角形、正四边形、正六边形的面积S3、S4、S6间的大小关系是( )
A. S3>S4>S6 B. S6>S4>S3 C. S6>S3>S4 D. S4>S6>S3
查看答案和解析>>
科目: 来源: 题型:
【题目】计算:(1)﹣7﹣1;
(2)(﹣3)+(﹣5)﹣(+11)﹣(﹣17);
(3)﹣3+8﹣7;
(4)(![]() )×(﹣24);
)×(﹣24);
(5)(![]() )×(﹣12);
)×(﹣12);
(6)(﹣0.1)﹣(﹣8![]() )+(﹣11
)+(﹣11![]() )﹣(﹣
)﹣(﹣![]() );
);
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料:我们知道|a|的几何意义是在数轴上数a对应的点与原点的距离,即|a|=|a﹣0|,也就是说,|a|表示在数轴上数a与数0对应点之间的距离.这个结论可以推广为:|a﹣b|表示在数轴上数a与b对应点之间的距离.
例1 已知|a|=2,求a的值.
解:在数轴上与原点距离为2的点的对应数为﹣2和2,即a的值为2和﹣2.
例2 已知|a﹣1|=2,求a的值.
解:在数轴上与1的距离为2点的对应数为3和﹣1,即a的值为3和﹣1.
仿照阅读材料的解法,解决下列问题:
(1)已知|a|=![]() ,求a的值;
,求a的值;
(2)已知|a+2|=4,求a的值;
(3)若数轴上表示a的点在﹣4与2之间,则|a+4|+|a﹣2|的值为 ;
(4)当a满足 时,则|a+4|+|a﹣2|的值最小,最小值是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,六边形ABCDEF的内角都相等, ![]() ,则下列结论成立的个数是
,则下列结论成立的个数是![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]() 四边形ACDF是平行四边形;
四边形ACDF是平行四边形; ![]() 六边形ABCDEF既是中心对称图形,又是轴对称图形.
六边形ABCDEF既是中心对称图形,又是轴对称图形.
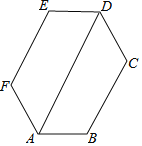
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目: 来源: 题型:
【题目】元旦放假时,小明一家三口一起乘小轿车去探望爷爷、奶奶和姥爷、姥姥.早上从家里出发,向东走了5千米到超市买东西,然后又向东走了2.5千米到爷爷家,下午从爷爷家出发向西走了10千米到姥爷家,晚上返回家里.
(1)若以小明家为原点,向东为正方向,用1个单位长度表示1千米,请将超市、爷爷家和姥爷家的位置在下面数轴上分别用点A、B、C表示出来;
![]()
(2)超市和姥爷家相距多少千米?
(3)若小轿车每千米耗油0.08升,求小明一家从出发到返回家,小轿车的耗油量.
查看答案和解析>>
科目: 来源: 题型:
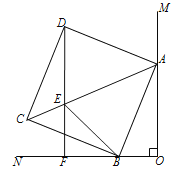
【题目】如图,∠MON=90°,正方形ABCD的顶点A、B分别在OM、ON上,AB=13,OB=5,E为AC上一点,且∠EBC=∠CBN,直线DE与ON交于点F.
(1)求证BE=DE;
(2)判断DF与ON的位置关系,并说明理由;
(3)△BEF的周长为 .
查看答案和解析>>
科目: 来源: 题型:
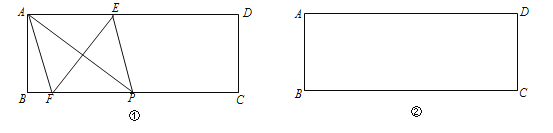
【题目】如图,在矩形ABCD中,AB=1,BC=3.
(1)在图①中,P是BC上一点,EF垂直平分AP,分别交AD、BC边于点E、F,求证:四边形AFPE是菱形;
(2)在图②中利用直尺和圆规作出面积最大的菱形,使得菱形的四个顶点都在矩形ABCD的边上,并直接标出菱形的边长.(保留作图痕迹,不写作法)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.

(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,DE是△ABC的中位线,AF是△ABC的中线.
求证DE=AF.

证法1:∵DE是△ABC的中位线,
∴DE= .
∵AF是△ABC的中线,∠BAC=90°,
∴AF= ,
∴DE=AF.
请把证法1补充完整,并用不同的方法完成证法2.
证法2:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com