
科目: 来源: 题型:
【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,
(1)写出数轴上点B表示的数 ;
(2)|5﹣3|表示5与3之差的绝对值,实际上也可理解为5与3两数在数轴上所对的两点之间的距离.如|x﹣3|的几何意义是数轴上表示有理数x的点与表示有理数3的点之间的距离.试探索:
①:若|x﹣8|=2,则x= .
②:|x+12|+|x﹣8|的最小值为 .
(3)动点P从O点出发,以每秒5个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.求当t为多少秒时?A,P两点之间的距离为2;
(4)动点P,Q分别从O,B两点,同时出发,点P以每秒5个单位长度沿数轴向右匀速运动,Q点以P点速度的两倍,沿数轴向右匀速运动,设运动时间为t(t>0)秒.问当t为多少秒时?P,Q之间的距离为4.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读第①小题的计算方法,再计算第②小题.
①–5![]() +(–9
+(–9![]() )+17
)+17![]() +(–3
+(–3![]() )
)
解:原式=[(–5)+(–![]() )]+[(–9)+(–
)]+[(–9)+(–![]() )]+(17+
)]+(17+![]() )+[(–3+(–
)+[(–3+(–![]() )]
)]
=[(–5)+(–9)+(–3)+17]+[(–![]() )+(–
)+(–![]() )+(–
)+(–![]() )+
)+![]() ]
]
=0+(–1![]() )
)
=–1![]() .
.
上述这种方法叫做拆项法.灵活运用加法的交换律、结合律可使运算简便.
②仿照上面的方法计算:(﹣2000![]() )+(﹣1999
)+(﹣1999![]() )+4000
)+4000![]() +(﹣1
+(﹣1![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC是直角三角形,∠ACB=90°.
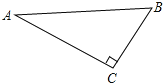
(1)尺规作图:作⊙C,使它与AB相切于点D,与AC相交于点E,保留作图痕迹,不写作法,请标明字母.
(2)在你按(1)中要求所作的图中,若BC=3,∠A=30°,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校准备购买A、B两种型号篮球,询问了甲、乙两间学校了解这两款篮球的价格,下表是甲、乙两间学校购买A、B两种型号篮球的情况:
购买学校 | 购买型号及数量(个) | 购买支出款项(元) | |
A | B | ||
甲 | 3 | 8 | 622 |
乙 | 5 | 4 | 402 |
(1)求A、B两种型号的篮球的销售单价;
(2)若该学校准备用不多于1000元的金额购买这两种型号的篮球共20个,求A种型号的篮球最少能采购多少个?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是用火柴棍摆成边长分别是1、2、3根火柴棍时的正方形,当边长为n根火柴棍时,若摆出的正方形所用的火柴棍的根数为S,则S= (用含n的代数式表示,n为正整数).
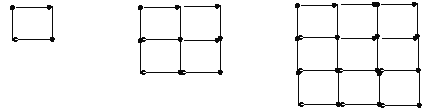
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,点0是AC边上一动点,过点0作DE,使DE∥BC,DE交∠ACB的角平分线于点D,交∠ACB的外角平分线于点E.
(1)求证:OD=OE;
(2)当点0运动到何处时,四边形CDAE是矩形?请证明你的结论.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=3cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,求EF和AE的长.
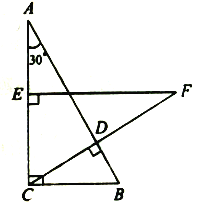
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于E,OD⊥BC交⊙O于D,DE交BC于F,点P为CB延长线上的一点,PE延长交AC于G,PE=PF,下列4个结论:①GE=GC;②AG=GE;③OG∥BE;④∠A=∠P.其中正确的结论是_____(填写所有正确结论的序号)
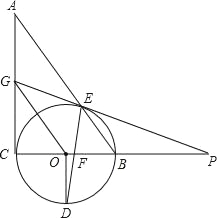
查看答案和解析>>
科目: 来源: 题型:
【题目】观察下面三行数
3,9,27,81…①
1,3,9,27…②
2,10,26,82…③
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
(3)设x,y,z分别为第①②③ 行的2019个数,求![]() 的值
的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com