小刚同学在学习完“圆”这一章内容后，感觉到一些几何问题，如果添加辅助圆，运用圆的知识解决，可以使问题变得非常容易．

例如：如图，在中，，，是外一点，且，求的度数，若以点为圆心，为半径作辅助圆⊙，则点、必在⊙上，是⊙的圆心角，而是圆周角，从而可容易得到__________．

（2）（问题解决）

如图，在四边形中，，，求的度数．

小刚同学认为用添加辅助圆的方法，可以使问题快速解决，他是这样思考的：的外接圆就是以的中点为圆心，长为半径的圆；的外接圆也是以的中点为圆心，长为半径的圆．这样、、、四点在同一个圆上，进而可以利用圆周角的性质求出的度数，请运用小刚的思路解决这个问题．

（3）（问题拓展）

如图，在中，，是边上的高，且，，求的长．

(1)若BD＝h，M是直线BC上的任意一点，M到AB、AC的距离分别为h1，h2．

A、若M在线段BC上，请你结合图形①证明：h1+h2＝h；

B、当点M在BC的延长线上时，h1，h2，h之间的关系为　 　．(请直接写出结论，不必证明)

(2)如图②，在平面直角坐标系中有两条直线l1：y＝x+6；l2：y＝﹣3x+6．若l2上的一点M到l1的距离是2，请你利用以上结论求解点M的坐标．

(1)这两次各购进这种衬衫多少件？

(2)若第一批衬衫的售价是200元/件，老板想让这两批衬衫售完后的总利润不低于2100元，则第二批衬衫每件至少要售多少元？

【题目】如图，在中，．

（1）先作的平分线交边于点，再以点为圆心，长为半径作⊙．

（要求：尺规作图，保留作图痕迹，不写作法）

（2）请你判断（1）中与⊙的位置关系，并证明你的结论．

（3）若，，求出（1）中⊙的半径．

(1)求证AD=ED；

(2)若AC=AB，DE=3，求AC的长．

(1)请在图中的网格平面内建立平面直角坐标系；

(2)请画出△ABC向右平移6个单位的△A1B1C1，并写出C1的坐标　 　；

(3)请画出△ABC关于原点O对称的△A2B2C2 ， 并写出点C2的坐标　 　．

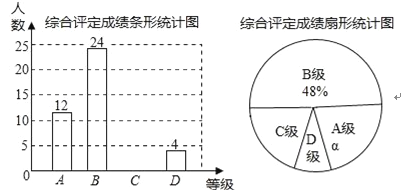
（1）在这次调查中，一共抽取了 名学生，α= %；

（2）补全条形统计图；

（3）扇形统计图中C级对应的圆心角为 度；

（4）若该校共有2000名学生，请你估计该校D级学生有多少名？

（1）小明购买A书，再从其余三本书中随机选一款，恰好选中C的概率是_________;

（2）小明随机选取两本书，请用树状图或列表法求出他恰好选中A、C两本的概率．

【题目】在学习绝对值后，我们知道，表示数在数轴上的对应点与原点的距离. 如：表示5在数轴上的对应点到原点的距离．而，即表示5、0在数轴上对应的两点之间的距离.类似的，有：表示5、3在数轴上对应的两点之间的距离；，所以表示5、在数轴上对应的两点之间的距离. 一般地，点A、B在数轴上分别表示有理数、，那么A、B之间的距离可表示为．

请根据绝对值的意义并结合数轴解答下列问题：

（1）数轴上表示2和5的两点之间的距离是______；数轴上表示1和－3的两点之间的距离是 ；

（2）数轴上P、Q两点的距离为3，且点P表示的数是2，则点Q表示的数是___________.

（3）点A、B、C在数轴上分别表示有理数、、1，那么A到B的距离与A到C的距离之和可表示为 ；

（4）满足的整数的值为 .

（5）的最小值为 .

(1)；

(2).