
科目: 来源: 题型:
【题目】如图,数轴的单位长度为1.
![]()
(1)如果点A,D表示的数互为相反数,那么点B表示的数是多少?
(2)如果点B,D表示的数互为相反数,那么图中表示的四个点中,哪一点表示的数的绝对值最大?为什么?
(3)当点B为原点时,若存在一点M到A的距离是点M到D的距离的2倍,则点M所表示的数是____.
查看答案和解析>>
科目: 来源: 题型:
【题目】先化简,再求值:
阅读材料,大数学家高斯在上学读书时曾经研究过这样一个问题:1+2+3+…+100=?经过研究,这个问题的一般性结论是1+2+3+…+![]() ,其中n是正整数。现在我们来研究一个类似的问题:1×2+2×3+…
,其中n是正整数。现在我们来研究一个类似的问题:1×2+2×3+…![]() =?
=?
观察下面三个特殊的等式
![]()
![]()
![]()
将这三个等式的两边相加,可以得到1×2+2×3+3×4=![]()
读完这段材料,请你思考后回答:(只需写出结果,不必写中间的过程)
(1)![]()
(2)1×2+2×3+3×4+…+n×(n+1)=
(3)![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数轴上的点A和点B之间的距离为28个单位长度,点A在原点的左边,距离原点8个单位长度,点B在原点的右边.
(Ⅰ)求点A,点B对应的数;
(Ⅱ)数轴上点A以每秒1个单位长度出发向左移动,同时点B以每秒3个单位长度的速度向左移动,在点C处追上了点A,求点C对应的数.
(Ⅲ)已知在数轴上点M从点A出发向右运动,速度为每秒1个单位长度,同时点N从点B出发向右运动,速度为每秒2个单位长度,设线段NO的中点为P(O为原点),在运动的过程中,线段![]() 的值是否变化?若不变,请说明理由并求其值;若变化,请说明理由.
的值是否变化?若不变,请说明理由并求其值;若变化,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
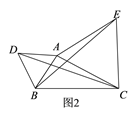
【题目】问题提出
![]() 如图1,点A为线段BC外一动点,且
如图1,点A为线段BC外一动点,且![]() ,填空:当点A位于______时,线段AC的长取得最大值,且最大值为______
,填空:当点A位于______时,线段AC的长取得最大值,且最大值为______![]() 用含
用含![]() 的式子表示
的式子表示![]() .
.
问题探究
![]() 点A为线段BC外一动点,且
点A为线段BC外一动点,且![]() ,如图2所示,分别以
,如图2所示,分别以![]() 为边,作等边三角形ABD和等边三角形ACE,连接
为边,作等边三角形ABD和等边三角形ACE,连接![]() ,找出图中与BE相等的线段,请说明理由,并直接写出线段BE长的最大值.
,找出图中与BE相等的线段,请说明理由,并直接写出线段BE长的最大值.
问题解决:
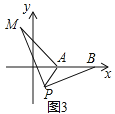
![]() 如图3,在平面直角坐标系中,点A的坐标为
如图3,在平面直角坐标系中,点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,点P为线段AB外一动点,且
,点P为线段AB外一动点,且![]() ,求线段AM长的最大值及此时点P的坐标.
,求线段AM长的最大值及此时点P的坐标.
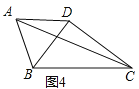
![]() 如图4,在四边形ABCD中,
如图4,在四边形ABCD中, ![]() ,若对角线
,若对角线![]() 于点D,请直接写出对角线AC的最大值.
于点D,请直接写出对角线AC的最大值.

查看答案和解析>>
科目: 来源: 题型:
【题目】某股民在上星期买进某种股票1000股,每股100元,下表是本周每日该股票的涨跌情况 (单位:元):

(1)该股在本周内最高价是每股多少元?最低价是每股多少元?
(2)星期三收盘时,每股是多少元?
(3)已知买进股票时需付成交额的1.5‰的手续费,卖出时需付成交额的1.5‰手续费和 1‰的交易费,如果在星期五收盘前将股票一次性卖出,他的收益情况如何?
查看答案和解析>>
科目: 来源: 题型:
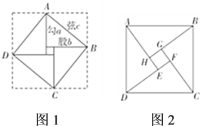
【题目】阅读下列材料并完成任务:
中国古代三国时期吴国的数学家赵爽最早对勾股定理作出理论证明.他创制了一幅“勾股圆方图”(如图l),用数形结合的方法,给出了勾股定理的详细证明.在这幅“勾股圆方图”中,以弦为边长得到的正方形![]() 是由
是由![]() 个全等的直角三角形再加上中间的那个小正方形组成的.每个直角三角形的面积为
个全等的直角三角形再加上中间的那个小正方形组成的.每个直角三角形的面积为![]() ;中间的小正方形边长为
;中间的小正方形边长为![]() ,面积为
,面积为![]() .于是便得到式子:
.于是便得到式子:![]() .赵爽的这个证明可谓别具匠心,极富创新意识.他用几何图形的截、割、拼、补来证明代数式之间的恒等关系,既具严密性,又具直观性,为中国古代以形证数、形数统一、代数和几何紧密结合、互不可分的独特风格树立了一个典范.如图2,是“赵爽弦图”,其中
.赵爽的这个证明可谓别具匠心,极富创新意识.他用几何图形的截、割、拼、补来证明代数式之间的恒等关系,既具严密性,又具直观性,为中国古代以形证数、形数统一、代数和几何紧密结合、互不可分的独特风格树立了一个典范.如图2,是“赵爽弦图”,其中![]() 、
、![]() 、
、![]() 和
和![]() 是四个全等的直角三角形,四边形
是四个全等的直角三角形,四边形![]() 和
和![]() 都是正方形,根据这个图形的面积关系,可以证明勾股定理.设
都是正方形,根据这个图形的面积关系,可以证明勾股定理.设![]() ,
,![]() ,
,![]() ,取
,取![]() ,
,![]() .
.
任务:
(1)填空:正方形![]() 的面积为______,四个直角三角形的面积和为______;
的面积为______,四个直角三角形的面积和为______;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为打造“书香校园”,学校每个班级都建立了图书角.七年1班,除了班上每位同学捐出一本书外,三位班委还相约图书城,用班费买些新书.下面是他们的对话内容:

(1)班委A上次买的一套书,图书城的利润是 元,利润率是 .如果当时他买一张会员卡,可省下 元.
(2)当购书的总价(指未打折前的原价)为多少时,办贵宾卡与办会员卡购书一样优惠?
(3)三个班委精心挑选了一批新书,经过计算分析后,发现三种购买方式中,办会员卡购书最省钱,请你直接写出这批书的总价的范围.
查看答案和解析>>
科目: 来源: 题型:
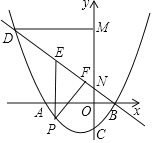
【题目】如图,抛物线![]() 与x轴交于A、B两点,其中点
与x轴交于A、B两点,其中点![]() ,交y轴于点
,交y轴于点![]() 直线
直线![]() 过点B与y轴交于点N,与抛物线的另一个交点是D,点P是直线BD下方的抛物线上一动点
过点B与y轴交于点N,与抛物线的另一个交点是D,点P是直线BD下方的抛物线上一动点![]() 不与点B、D重合
不与点B、D重合![]() ,过点P作y轴的平行线,交直线BD于点E,过点D作
,过点P作y轴的平行线,交直线BD于点E,过点D作![]() 轴于点M.
轴于点M.
![]() 求抛物线
求抛物线![]() 的表达式及点D的坐标;
的表达式及点D的坐标;
![]() 若四边形PEMN是平行四边形?请求出点P的坐标;
若四边形PEMN是平行四边形?请求出点P的坐标;
![]() 过点P作
过点P作![]() 于点F,设
于点F,设![]() 的周长为C,点P的横坐标为a,求C与a的函数关系式,并求出C的最大值.
的周长为C,点P的横坐标为a,求C与a的函数关系式,并求出C的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com