
科目: 来源: 题型:
【题目】将下列各数填入相应的集合内:
![]() ,1.010010001,
,1.010010001,![]() ,22,-8,
,22,-8,![]() ,-1.232232223…,-1.414,0.
,-1.232232223…,-1.414,0.
正数集合{ ……}
负数集合{ ……}
有理数集合{ ……}
无理数集合{ ……}
查看答案和解析>>
科目: 来源: 题型:
【题目】包装厂有工人42人,每个工人平均每小时可以生产圆形铁片120片,或长方形铁片80片,两张圆形铁片与一张长方形铁片可配套成一个密封圆桶,问每天如何安排工人生产圆形和长方形铁片能合理地将铁片配套?设安排x人生产圆形铁片,可以列方程:( )
A.120(42﹣x)=2×80xB.80(42﹣x)=120x
C.2×80(42﹣x)=120xD.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:四边形ABCD,E,F,G,H是各边的中点.
(1)求证:四边形EFGH是平行四边形;
(2)假如四边形ABCD是一个矩形,猜想四边形EFGH是什么图形?并证明你的猜想.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知函数y=x+1和y=ax+3的图象交于点P,点P的横坐标为1,
(1)关于x,y的方程组![]() 的解是 ;
的解是 ;
(2)a= ;
(3)求出函数y=x+1和y=ax+3的图象与x轴围成的几何图形的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在数轴上A、B两点对应的数分别是6,-6,∠DCE=90°(C与O重合,D点在数轴的正半轴上)

(1)如图1,若CF平分∠ACE,则∠AOF=_______;
(2)如图2,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α.
①当t=1时,α=_________;
②猜想∠BCE和α的数量关系,并证明;
(3)如图3,开始∠D1C1E1与∠DCE重合,将∠DCE沿数轴正半轴向右平移t(0<t<3)个单位,再绕顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t(0<t<3)个单位,再绕顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1,记∠D1C1F1=β,若α,β满足|α-β|=45°,请用t的式子表示α、β并直接写出t的值.
查看答案和解析>>
科目: 来源: 题型:
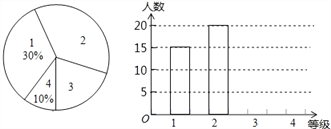
【题目】新的交通法规实施后,驾校的考试规则也发生了变化,考试共设四个科目:科目1、科目2、科目3和科目4,以下简记为:1、2、3、4.四个科目考试在同一地点进行,但每个学员每次只能够参加一个科目考试.在某次考试中,对该考点各科目考试人数进行了调查统计,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:
(1)本次被调查的学员共有 人;在被调查者中参加“科目3”测试的有 人;将条形统计图补充完整;
(2)该考点参加“科目4”考试的学员里有3位是教师,某新闻部门准备在该考点参加“科目4”考试的学员中随机选出2位,调查他们对新规的了解情况,请你用列表法或画树状图的方法求出所选两位学员恰好都是教师的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知数轴上有A、B两点(点A在点B的左侧),且两点距离为8个单位长度,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
![]()
(1)图中如果点A、B表示的数是互为相反数,那么点A表示的数是 ;
(2)当t=3秒时,点A与点P之间的距离是 个长度单位;
(3)当点A表示的数是-3时,用含t的代数式表示点P表示的数;
(4)若点P到点A的距离是点P到点B的距离的2倍,请直接写出t的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】一分钟投篮测试规定,得6分以上为合格,得9分以上为优秀,甲、乙两组同学的一次测试成绩如下:
成绩(分) | 4 | 5 | 6 | 7 | 8 | 9 |
甲组(人) | 1 | 2 | 5 | 2 | 1 | 4 |
乙组(人) | 1 | 1 | 4 | 5 | 2 | 2 |
(1)请你根据上述统计数据,把下面的图和表补充完整;

一分钟投篮成绩统计分析表:
统计量 | 平均分 | 方差 | 中位数 | 合格率 | 优秀率 |
甲组 | 2.56 | 6 | 80.0% | 26.7% | |
乙组 | 6.8 | 1.76 | 86.7% | 13.3% |
(2)下面是小明和小聪的一段对话,请你根据(1)中的表,写出两条支持小聪的观点的理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】.如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线![]() 相交于点A(m,3),B(-6,n),与x轴交于点C.
相交于点A(m,3),B(-6,n),与x轴交于点C.
(1)求直线y=kx+b(k≠0)的解析式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标(直接写出结果).
S△BOC,求点P的坐标(直接写出结果).

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)探究:线段OE与OF的数量关系并加以证明;
(2)当点O运动到何处时,且△ABC满足什么条件时,四边形AECF是正方形?
(3)当点O在边AC上运动时,四边形BCFE 是菱形吗?(填“可能”或“不可能”)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com