
����Ŀ��һ����Ͷ�����Թ涨����6������Ϊ�ϸ�9������Ϊ���㣬�ס�������ͬѧ��һ�β��Գɼ����£�
�ɼ����֣� | 4 | 5 | 6 | 7 | 8 | 9 |
���飨�ˣ� | 1 | 2 | 5 | 2 | 1 | 4 |
���飨�ˣ� | 1 | 1 | 4 | 5 | 2 | 2 |
��1�������������ͳ�����ݣ��������ͼ�ͱ�����������

һ����Ͷ���ɼ�ͳ�Ʒ�������
ͳ���� | ƽ���� | ���� | ��λ�� | �ϸ��� | ������ |
���� | 2.56 | 6 | 80.0% | 26.7% | |
���� | 6.8 | 1.76 | 86.7% | 13.3% |
��2��������С����С�ϵ�һ�ζԻ���������ݣ�1���еı���д������֧��С�ϵĹ۵�����ɣ�

���𰸡�(1)����������2������ɼ����ڼ��飬���ɼ�����
��������
��1�����ݲ��Գɼ����������ɼ�Ϊ7�ֺ�9�ֵ���������ȫͳ��ͼ���ٸ���ƽ�����ļ��㷽������λ���Ķ������ƽ��������λ�������ɲ�ȫ��������
��2������ƽ���֡������λ�����ϸ��ʵ����弴��д��֧��С�ϵĹ۵�����ɣ�
��1�����ݲ��Գɼ������ɲ�ȫͳ��ͼ����ͼ����
��ȫ������������ƽ���֣�4��1+5��2+6��5+7��2+8��1+9��4����15��6.8��
������λ���ǵ�8��������7��
ͳ���� | ƽ���� | ���� | ��λ�� | �ϸ��� | ������ |
���� | 6.8 | 2.56 | 6 | 80.0% | 26.7% |
���� | 6.8 | 1.76 | 7 | 86.7% | 13.3% |

��2����������ƽ����һ��������ķ�����ڼ��飬˵������ɼ��ȼ����ȶ���������ϸ��ʱȼ���ߣ���������ɼ����ڼ��飮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=��x+10��x�ᡢy��ֱ��ڵ�B��C����A������Ϊ��8��0����P��x��y����ֱ��y=��x+10�ڵ�һ������һ�����㣮
��1�����OPA�����S��x�ĺ�����ϵʽ����д���Ա�����x��ȡֵ��Χ��
��2������OPA�����Ϊ10ʱ�����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������κ���![]() ��ͼ������ύ�ڵ�A����2,0��,B��3,0����������A��������������
��ͼ������ύ�ڵ�A����2,0��,B��3,0����������A��������������![]() ��ͼ��ĶԳƵ�ΪC��
��ͼ��ĶԳƵ�ΪC��
��1����b��c��ֵ��
��2��֤������C ������Ķ��κ�����ͼ���ϣ�
��3����ͼ��������B��DB�����ύ����������![]() ��ͼ���ڵ�D������AC��������������
��ͼ���ڵ�D������AC��������������![]() ��ͼ���ڵ�E������AD��CD���������P�ӵ�A���߶�AD������ÿ��2����λ���ٶ����D�˶���ͬʱ����Q�ӵ�D���߶�DC������ÿ��1����λ���ٶ����C�˶���������һ�������յ�ʱ����һ����ֹ֮ͣ�˶�������PQ��QE��PE�����˶�ʱ��Ϊt�룬�Ƿ����ijһʱ�̣�ʹPEƽ����APQ��ͬʱQEƽ����PQC�������ڣ����t��ֵ���������ڣ���˵�����ɡ�
��ͼ���ڵ�E������AD��CD���������P�ӵ�A���߶�AD������ÿ��2����λ���ٶ����D�˶���ͬʱ����Q�ӵ�D���߶�DC������ÿ��1����λ���ٶ����C�˶���������һ�������յ�ʱ����һ����ֹ֮ͣ�˶�������PQ��QE��PE�����˶�ʱ��Ϊt�룬�Ƿ����ijһʱ�̣�ʹPEƽ����APQ��ͬʱQEƽ����PQC�������ڣ����t��ֵ���������ڣ���˵�����ɡ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C���߶�AB�ϣ�����C��CD��AB����E��F�ֱ���AD��CD���е㣬����EF���ӳ�EF����G��ʹ��FG=CB������CE��GB������B��BH��CE���߶�EG�ڵ�H��
��1����֤���ı���FCBG�Ǿ��Σ�
��2����֪AB=10��![]() ��
��
�ٵ��ı���ECBH������ʱ����EG�ij���
������CH��DH���ǡ�DEH�����ΪS1�� ��CBH�����ΪS2����EG=2FH����S1+S2��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����ǰ�������ڽǷֱ���90![]() ,45
,45![]() ,45
,45![]() ��90
��90![]() ,60
,60![]() ,30
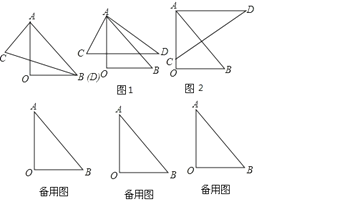
,30![]() ,����ͼ��ʾ������һ��,���̶�������AOB,�ı�������ACD��λ��(���е�Aλ��ʼ�ղ���),���ڳɲ�ͬ��λ��,ʹ�������ǰ�������һ���ƽ�С����BAD=��(0
,����ͼ��ʾ������һ��,���̶�������AOB,�ı�������ACD��λ��(���е�Aλ��ʼ�ղ���),���ڳɲ�ͬ��λ��,ʹ�������ǰ�������һ���ƽ�С����BAD=��(0![]() <��<180
<��<180![]() )
)
(1)��ͼ1��,����̽������Ϊ����ʱ,CD��OB����˵�����ɣ�
(2)��ͼ2��,����=___ʱ,AD��OB��
(3)�ڵ�Aλ��ʼ�ղ��������£��㻹�ܰڳɼ��ֲ�ͬ��λ�ã�ʹ�������ǰ���������һ���ƽ�У���ֱ��д������Ҫ������Ķ�������д���������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ı���ABCD��E��F��G��H�Ǹ��ߵ��е㣮
��1����֤���ı���EFGH��ƽ���ı��Σ�
��2�������ı���ABCD��һ�����Σ������ı���EFGH��ʲôͼ�Σ���֤����IJ��룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һЩ�뾶��ͬ��СԲ����ͼ��ʾ�Ĺ��ɰڷţ���1��ͼ����6��СԲ����2��ͼ����10��СԲ����3��ͼ����16��СԲ����4��ͼ����24��СԲ�������˹��ɣ���7��ͼ�ε�СԲ�ĸ�����_____����n��ͼ�ε�СԲ�ĸ�����_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A��B�������Ϸֱ��ʾ������a��b��A��B����֮��ľ����ʾΪAB����������A��B����֮��ľ���AB��|a��b|���������ν��˼��ش��������⣺
��1�������ϱ�ʾ��2��8����֮��ľ�����________��
��2�������ϱ�ʾx�ͩ�4����A��B֮��ľ����ʾΪ__________�����AB��2����ôx��___________��
(3)����C��ʾ����Ϊx,����C��ʲôλ��ʱ,|![]() x+1|+|
x+1|+|![]() x1|ȡ�õ�ֵ��С����ֱ��д����Сֵ��
x1|ȡ�õ�ֵ��С����ֱ��д����Сֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com