
科目: 来源: 题型:
【题目】学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?

查看答案和解析>>
科目: 来源: 题型:
【题目】![]() .
.![]() 分别是数轴上两个不同点A.B所表示的有理数,且
分别是数轴上两个不同点A.B所表示的有理数,且![]() ,
,![]() ,A.B两点在数轴上的位置如图所示:
,A.B两点在数轴上的位置如图所示:
(1)数![]() =_____;
=_____;![]() =______;
=______;
(2)A.B两点相距多少个单位长度?
(3)点P从A点出发,先向左移动一个单位长度,再向右移动2个单位长度,再向左移动3个单位长度,再向右移动4个单位长度,依次操作2020次后,求P点表示的数.
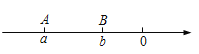
查看答案和解析>>
科目: 来源: 题型:
【题目】某食品厂计划平均每天生产200袋食品,但是由于种种原因,实际每天生产量与计划量相比有出入,下表是某周的生产情况(超过计划量记为正):

(1)根据记录的数据可知产量最多的一天比产量最少的一天多生产食品多少袋?
(2)根据记录的数据可知该厂本周实际共生产食品多少袋?
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两家商场以同样的价格出售同样的电器,但各自推出的优惠方案不同,甲商场规定:凡超过![]() 元的电器,超出的金额按
元的电器,超出的金额按![]() 收取;乙商场规定:凡超过
收取;乙商场规定:凡超过![]() 元的电器,超出的金额按
元的电器,超出的金额按![]() 收取,某顾客购买的电器价格是
收取,某顾客购买的电器价格是![]() 元.
元.
(1)当![]() 时,分别用代数式表示在两家商场购买电器所需付的费用
时,分别用代数式表示在两家商场购买电器所需付的费用
(2)当![]() 时,该顾客应选择哪一家商场购买比较合算?说明理由.
时,该顾客应选择哪一家商场购买比较合算?说明理由.
查看答案和解析>>
科目: 来源: 题型:
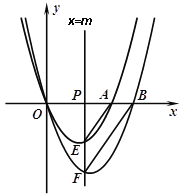
【题目】如图,动直线![]() (
(![]() )分别交x轴,抛物线
)分别交x轴,抛物线![]() 和
和![]() 于点P,E,F,设点A,B为抛物线
于点P,E,F,设点A,B为抛物线![]() ,
, ![]() 与x轴的一个交点,连结AE,BF.
与x轴的一个交点,连结AE,BF.
(1)求点A,B的坐标.
(2)当![]() 时,判断直线AE与BF的位置关系,并说明理由.
时,判断直线AE与BF的位置关系,并说明理由.
(3)连结BE,当![]() 时,求△BEF的面积.
时,求△BEF的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市居民使用自来水按如下标准收费(水费按月缴纳)
户月用水量 | 单价 |
不超过 | 2元/ |
超过 | 3元/ |
超过 | 4元/ |
(1)某用户一个月用了![]() 水,则该用户缴纳的水费是______元;
水,则该用户缴纳的水费是______元;
(2)某户月用水量为![]() 立方米(10<x≤20),该用户缴纳的水费是______元(用含
立方米(10<x≤20),该用户缴纳的水费是______元(用含![]() 的整式表示)
的整式表示)
(3)一月份甲、乙两用户共用水![]() ,设甲用户用水量为
,设甲用户用水量为![]() ,且
,且![]() ,若他们这个月共付水费105元,求
,若他们这个月共付水费105元,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某农户共摘收水蜜桃1920千克,为寻求合适的销售价格,进行了6天试销,试销情况如下:
第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | |
售价 x(元/千克) | 20 | 18 | 15 | 12 | 10 | 9 |
销售量 y(千克) | 45 | 50 | 60 | 75 | 90 | 100 |
由表中数据可知,试销期间这批水蜜桃的每天销售量y(千克)与售价x(元/千克)之间满足我们曾经学过的某种函数关系.若在这批水蜜桃的后续销售中,每天的销售量y(千克)与售价x(元/千克)之间都满足这一函数关系.
(1)你认为y与x之间满足什么函数关系?并求y关于x的函数表达式.
(2)在试销6天后,该农户决定将这批水密桃的售价定为15元/千克.
① 若每天都按15元/千克的售价销售,则余下的水蜜桃预计还要多少天可以全部售完?
② 该农户按15元/千克的售价销售20天后,发现剩下的水蜜桃过于成熟,必须在不超过2天内全部售完,因此需要重新确定一个售价,使后面2天都按新的售价销售且能如期全部售完,则新的售价最高可以定为多少元/千克?
查看答案和解析>>
科目: 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AB=5,BC=3,点D、E分别在BC、AC上,且BD=CE,设点C关于DE的对称点为F,若DF∥AB,则BD的长为_______.

查看答案和解析>>
科目: 来源: 题型:
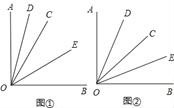
【题目】已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.
(1)如图①,当∠BOC=40°时,求∠DOE的度数;
(2)如图②,当射线OC在∠AOB内绕O点旋转时,∠DOE的大小是否发生变化,说明理由;
(3)当射线OC在∠AOB外绕O点旋转且∠AOC为钝角时,画出图形,直接写出∠DOE的度数(不必写过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com