
科目: 来源: 题型:
【题目】已知四边形ABCD为正方形,E是BC的中点,连接AE,过点A作∠AFD,使∠AFD=2∠EAB,AF交CD于点F,如图①,易证:AF=CD+CF.
(1)如图②,当四边形ABCD为矩形时,其他条件不变,线段AF,CD,CF之间有怎样的数量关系?请写出你的猜想,并给予证明;
(2)如图③,当四边形ABCD为平行四边形时,其他条件不变,线段AF,CD,CF之间又有怎样的数量关系?请直接写出你的猜想.
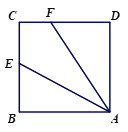
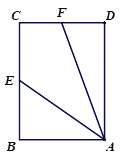
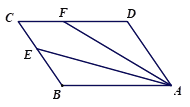
图① 图② 图③
查看答案和解析>>
科目: 来源: 题型:
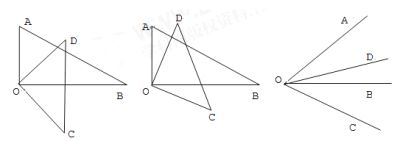
【题目】(1) 将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起, ∠AOB=∠DOC=90°.
①如图(1),若OD是∠AOB的平分线时,求∠BOD和∠AOC的度数.
②如图(2),若OD不是∠AOB的平分线,试猜想∠AOC与∠BOD的数量关系,并说明理由.
(2)如图(3),如果两个角∠AOB = ∠DOC= m°(0< m <90),直接写出∠AOC与∠BOD的数量关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是“用三角板画圆的切线”的画图过程.
如图1,已知圆上一点A,画过A点的圆的切线.
![]()

画法:(1)如图2,将三角板的直角顶点放在圆上任一点C(与点A不重合)处,使其一直角边经过点A,另一条直角边与圆交于B点,连接AB;
(2)如图3,将三角板的直角顶点与点A重合,使一条直角边经过点B,画出另一条直角边所在的直线AD.
所以直线AD就是过点A的圆的切线.
请回答:该画图的依据是_______________________________________________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为

A.![]() B.3 C.1 D.
B.3 C.1 D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】轮胎的直径是否符合标准,是判断轮胎质量的好与差的重要依据之一.东风轮胎厂某批轮胎的标准直径是600mm,质量检验员从这批产品中抽取10个轮胎进行检查,超过标准直径的毫米数记为正,不足的毫米数记为负,检查记录如下(单位:mm):
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
检查结果 |
|
|
| 0 |
|
|
|
|
|
|
(
(2)求这10个轮胎的平均直径(精确到![]() mm).
mm).
查看答案和解析>>
科目: 来源: 题型:
【题目】在2016年巴西里约奥运会上,中国女排克服重重困难,凭借顽强的毅力和超强的实力先后战胜了实力同样超强的巴西队,荷兰队和塞尔维亚队,获得了奥运冠军,为祖国和人民争了光.
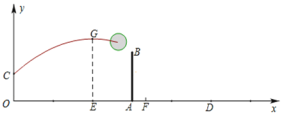
如图,已知女排球场的长度OD为18米,位于球场中线处的球网AB的高度为2.24米,一队员站在点O处发球,排球从点O的正上方2米的C点向正前方飞去,排球的飞行路线是抛物线的一部分,当排球运行至离点O的水平距离OE为6米时,到达最高点F,以O为原点建立如图所示的平面直角坐标系.
(1)当排球运行的最大高度为2.8米时,求排球飞行的高度y(单位:米)与水平距离x(单位:米)之间的函数关系式.
(2)在(1)的条件下,这次所发的球能够过网吗?如果能够过网,是否会出界?请说明理由.
(3)喜欢打排球的李明同学经研究后发现,发球要想过网,球运行的最大高度h(米)应满足h>2.32,但是他不知道如何确定h的取值范围,使排球不会出界(排球压线属于没出界),请你帮忙解决并指出使球既能过网又不会出界的h的取值范围 .
查看答案和解析>>
科目: 来源: 题型:
【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了多少名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数是多少?
(2)将条形统计图补充完整;
(3)该校共有900名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,升降平台由三个边长为1.2米的菱形和两个腰长为1.2米的等腰三角形组成,其中平台AM与底座A0N平行,长度均为24米,点B,B0分别在AM和A0N上滑动这种设计是利用平行四边形的________;为了安全,该平台作业时∠B1不得超过60°,则平台高度(AA0)的最大值为________米

查看答案和解析>>
科目: 来源: 题型:
【题目】在下列四项调查中,方式正确的是![]()
![]()
A. 了解本市中学生每天学习所用的时间,采用全面调查的方式
B. 为保证运载火箭的成功发射,对其所有的零部件采用抽样调查的方式
C. 了解某市每天的流动人口数,采用全面调查的方式
D. 了解全市中学生的视力情况,采用抽样调查的方式
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com