
科目: 来源: 题型:
【题目】《九章算术》卷九“勾股”中记载:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问霞长几何.
注释:今有正方形水池边长1丈,芦苇生长在中央,长出水面1尺.将芦苇向池岸牵引,恰好与水岸齐,问芦苇的长度(一丈等于10尺).解决下列问题:
(1)示意图中,线段![]() 的长为______尺,线段
的长为______尺,线段![]() 的长为______尺;
的长为______尺;

(2)求芦苇的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线![]() 的顶点C在x轴正半轴上,一次函数
的顶点C在x轴正半轴上,一次函数![]() 与抛物线交于A、B两点,与x、y轴交于D、E两点.
与抛物线交于A、B两点,与x、y轴交于D、E两点.

(1)求m的值.
(2)求A、B两点的坐标.
(3)点P(a,b)(![]() )是抛物线上一点,当△PAB的面积是△ABC面积的2倍时,求a,b的值.
)是抛物线上一点,当△PAB的面积是△ABC面积的2倍时,求a,b的值.
查看答案和解析>>
科目: 来源: 题型:
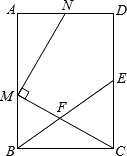
【题目】如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N.
(1)当F为BE中点时,求证:AM=CE;
(2)若![]() =2,求
=2,求![]() 的值;
的值;
(3)若![]() =n,当n为何值时,MN∥BE?
=n,当n为何值时,MN∥BE?
查看答案和解析>>
科目: 来源: 题型:
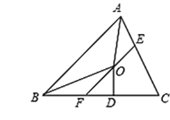
【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于点F,交AC于点E,过点O作OD⊥BC于D,下列四个结论:①∠AOB=90°+![]() ∠C;②AE+BF=EF;③当∠C=90°时,E、F分别是AC、BC的中点;④若OD=
∠C;②AE+BF=EF;③当∠C=90°时,E、F分别是AC、BC的中点;④若OD=![]() CE+CF=
CE+CF=![]() 则S△CEF=
则S△CEF=![]() ,其中正确的是______________
,其中正确的是______________
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知射线DE与x轴和y轴分别交于点D(3,0)和点E(0,4).动点C从点M(5,0)出发,以1个单位长度/秒的速度沿x轴向左作匀速运动,与此同时,动点P从点D出发,也以1个单位长度/秒的速度沿射线DE的方向作匀速运动,设运动时间为t秒,

(1)请用含t的代数式分别表示出点C与点P的坐标;
(2)以点C为中心,![]() 个单位长度为半径的⊙C与x轴交于A、B两点(点A在点B的左侧),连接PA、PB.
个单位长度为半径的⊙C与x轴交于A、B两点(点A在点B的左侧),连接PA、PB.
①当⊙C与射线DE有公共点时,求t的取值范围;
②当△PAB为等腰三角形时,求t的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】2台大收割机和5台小收割机同时工作2 h共收割小麦3.6hm2,3台大收割机和2台小收割机同时工作5 h共收割小麦8 hm2.1台大收割机和1台小收割机每小时各收割小麦多少公顷?
查看答案和解析>>
科目: 来源: 题型:
【题目】数学课上, 老师要求同学们利用三角板画两条平行线.老师说苗苗和小华两位同学画法都是正确的,两位同学的画法如下:
苗苗的画法:

①将含30°角的三角尺的最长边与直线a重合,另一块三角尺最长边与含30°角的三角尺的最短边紧贴;
②将含30°角的三角尺沿贴合边平移一段距离,画出最长边所在直线b,则b//a.
小华的画法:

①将含30°角三角尺的最长边与直线a重合,用虚线做出一条最短边所在直线;
②再次将含30°角三角尺的最短边与虚线重合,画出最长边所在直线b,则b//a.
请在苗苗和小华两位同学画平行线的方法中选出你喜欢的一种,并写出这种画图的依据.
答:我喜欢__________同学的画法,画图的依据是__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了决定谁将获得仅有的一张科普报告入场劵,甲和乙设计了如下的摸球游戏:在不透明的A、B两个口袋中分别放入编号分别为1,2,3的三个红球及一个白球,四个小球除了颜色和编号不同外,其他没有任何区别;甲在A口袋中摸出两个球,乙在B口袋中摸出一个球,如果甲摸出的两个球都是红色的甲得1分,否则,甲得0分,如果乙摸出的球是白色的,乙得1分,否则乙得0分,得分高的获得入场券,如果得分相同,游戏重来.
(1)运用列表或画树状图的方法求甲得1分的概率;
(2)请你用所学的知识说明这个游戏是否公平.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(6,4)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )

A. (2,12)
B. (﹣2,0)
C. (2,12)或(﹣2,0)
D. (12,2)或(﹣2,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com