
科目: 来源: 题型:
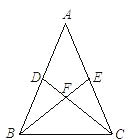
【题目】如图,在△ABC中,AB = AC,点D、E分别是AB、AC的中点,点F是BE、CD的交点,请写出图中两组全等的三角形,并选出其中一组加以证明.(要求:写出证明过程中的重要依据)
查看答案和解析>>
科目: 来源: 题型:
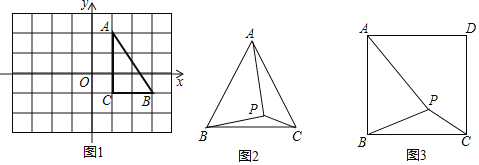
【题目】(1)如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′,则∠AB′B= ;
(2)如图2,在等边三角形ABC内有一点P,且PA=![]() ,PB=2,PC=
,PB=2,PC=![]() ,求∠BPC的度数和等边三角形ABC的边长;
,求∠BPC的度数和等边三角形ABC的边长;
(3)如图3,在正方形ABCD内有一点P,且PA=![]() ,PB=2,PC=
,PB=2,PC=![]() ,求∠BPC的度数和正方形ABCD的边长.
,求∠BPC的度数和正方形ABCD的边长.
查看答案和解析>>
科目: 来源: 题型:
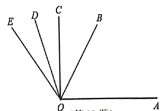
【题目】如图,已知:OB是∠AOE的平分线,OD是∠COE的平分线.
(1)若∠AOC= 90°,∠COE =30°,求∠BOD的度数;
(2)若(1)中的∠COE=α(α为锐角),其它条件不变,求∠BOD的度数;
(3)若(1)中的∠AOC=β,其它条件不变,求∠BOD的度数;
(4)从(1),(2),(3)的结果中猜想∠BOD与∠AOC的数量关系是________ ,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】计算:
(1)(+10)+(﹣4)
(2)(﹣![]() )+(﹣
)+(﹣![]() )+(﹣
)+(﹣![]() )+
)+![]() ;
;
(3)5.6+(﹣0.9)+4.4+(﹣8.1)
(4)(﹣81)÷![]() ×
×![]() ÷(﹣16)
÷(﹣16)
(5)(﹣5)×49![]()
(6)(﹣125)×[2﹣(﹣2)]﹣300÷6.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着互联网经济的发展,“共享单车“越来越走近老百姓的生活.赵刚同学对某站点”共享单车”的租用情况进行了调查,将该站点一天中市民每次租用“其享单车“的时间t(单位:分)(t≤120)分成A,B,C,D四个组,进行各组人次统计,并绘制了如下的统计图(不完整).请根据图中信息解答下列问题:

(1)该站点一天中租用”共享单车“的总人次为 ,表示A的扇形圆心角的度数是 .
(2)补全条形统计图.
(3)“共享单车”服务公司规定:市民每次使用共享单车时间不超过30分钟收费1元,超过30分钟收费2元,已知该市每天租用共享单车(时间在2小时以内)的市民平均约有5000人次,根据以上数据估计共享单车服务公司每天大约收入多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】把下列各数分别填人相应的集合里.
﹣5,﹣2.626626662…,0,﹣π,﹣![]() ,0.12,﹣(﹣6).
,0.12,﹣(﹣6).
(1)正数集合:{____________________…};
(2)无理数集合:{___________________ …};
(3)负整数集合:{__________________…};
(4)分数集合:{___________________ …}.
查看答案和解析>>
科目: 来源: 题型:
【题目】某通讯公司推出了移动电话的两种计费方式(详情见下表)。
月使用费/元 | 主叫限定时间/分 | 主叫超时费/(元/分) | 被叫 | |
方式一 | 58 | 150 | 0.25 | 免费 |
方式二 | 88 | 350 | 0.19 | 免费 |

设一个月内使用移动电话主叫的时间为![]() 分(
分(![]() 为正整数),请根据表中提供的信息回答下列问题:
为正整数),请根据表中提供的信息回答下列问题:
(1)用含有![]() 的式子填写下表:
的式子填写下表:
| 150< |
|
| |
方式一计费/元 | 58 |
| 108 |
|
方式二计费/元 | 88 | 88 | 88 |
|
(Ⅰ)当![]() 为何值时,两种计费方式的费用相等?
为何值时,两种计费方式的费用相等?
(Ⅱ)请根据(Ⅰ)和(Ⅱ)的计算及生活经验,直接写出不同时间段,选用哪种计费方式省钱.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,A(0,4),B(2,0),C(5,1),D(2,5).

(1)AD= ,AB= ;
(2)∠BAD是直角吗?请说出理由;
(3)求点B到直线CD的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线AB交x轴于点B(2,0),交y轴于点A(0,2),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=3,连接DA,∠DAC=90°.
(1)求直线AB的解析式.
(2)求D点坐标及过O、D、B三点的抛物线解析式.
(3)若点P是线段OB上的动点,过点P作x轴的垂线交AB于F,交(2)中抛物线于E,连CE,是否存在P使△BPF与△FCE相似?若存在,请求出P点坐标;若不存在说明理由.

查看答案和解析>>
科目: 来源: 题型:
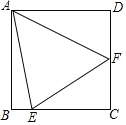
【题目】如图,在正方形ABCD中,AB=BC=CD=DA,∠BAD=∠ABC=∠BCD=∠ADC=90°,E、F为BC、CD边上的点,若∠FAE=45°,试探究线段BE、EF、DF之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com