
科目: 来源: 题型:
【题目】对非负实数x“四舍五入”到个位的值记为< x >,即已知n为正整数,如果n-![]() ≤x<n+
≤x<n+![]() ,那么< x >=n.例如:< 0 >=< 0.48 >=0,< 0.64 >=< 1.493 >=1,< 2 >=2,< 3.5 >=< 4.12 >=4,…则满足方程< x >=
,那么< x >=n.例如:< 0 >=< 0.48 >=0,< 0.64 >=< 1.493 >=1,< 2 >=2,< 3.5 >=< 4.12 >=4,…则满足方程< x >=![]() 的非负实数x的值为____.
的非负实数x的值为____.
查看答案和解析>>
科目: 来源: 题型:
【题目】在数轴上,表示数x的点到原点的距离用|x|表示,如果表示数m的点和﹣5的点之间的距离是3,那么m=_____;|c﹣![]() |+|c﹣4|+|c+1|的最小值是_____
|+|c﹣4|+|c+1|的最小值是_____
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°.
①若AB=CD=1,AB∥CD,求对角线BD的长.
②若AC⊥BD,求证:AD=CD;
(2)如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形,求AE的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.

(1)求∠BOD的度数;
(2)试判断OE是否平分∠BOC,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
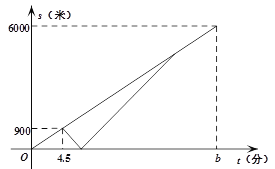
【题目】周末,甲、乙两名大学生骑自行车去距学校6000米的净月潭公园.两人同时从学校出发,以a米/分的速度匀速行驶出发4.5分钟时,甲同学发现忘记带学生证,以1.5a米/分的速度按原路返回学校,取完学生证(在学校取学生证所用时间忽略不计),继续以返回时的速度追赶乙.甲追上乙后,两人以相同的速度前往净月潭.乙骑自行车的速度始终不变.设甲、乙两名大学生距学校的路程为s(米),乙同学行驶的时间为t(分),s与t之间的函数图象如图所示.
(1)求a、b的值.
(2)求甲追上乙时,距学校的路程.
(3)当两人相距500米时,直接写出t的值是_______________.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)观察下列各式:
![]() ……试用你发现的规律填空:
……试用你发现的规律填空:![]() ,
,![]() 。
。
(2)请你用含有一个字母的等式将上面各式呈现的规律表示出来,并用所学数学知识说明你所写式子的正确性。
查看答案和解析>>
科目: 来源: 题型:
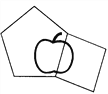
【题目】一个正五边形与一个正方形的边长正好相等,在它们相接的地方,形成一个完整的“苹果”图案(如图).如果让正方形沿着正五边形的四周滚动,并且始终保持正方形和正五边形有两条边邻接,那么第一次恢复“苹果”的图形时,正方形要绕五边形转( )圈.
A. 4 B. 3 C. 6 D. 8
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在数轴上点A表示的有理数为-6,点B表示的有理数为4,点P从点A出发,以每秒2个单位长度的速度在数轴上向点B运动,当点P到达点B后立即返回,仍然以每秒2个单位长度的速度运动至点A停止.设运动时间为t(单位:秒).
(1)求t=1时点P表示的有理数;
(2)求点P与点B重合时的t值;
(3)在点P沿数轴由点A到点B再回到点A的运动过程中,求点P与点A的距离(用含t的代数式表示);
(4)当点P表示的有理数与原点的距离是2个单位长度时,直接写出所有满足条件的t值.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某市政府规定:若本市企业按生产成本价提供产品给大学生销售,则政府给该企业补偿![]() 补偿额
补偿额![]() 批发价
批发价![]() 生产成本价
生产成本价![]() 销售量
销售量![]() 大学生小明投资销售本市企业生产的一种新型节能灯,调查发现,每月销售量
大学生小明投资销售本市企业生产的一种新型节能灯,调查发现,每月销售量![]() 件
件![]() 与销售单价
与销售单价![]() 元
元![]() 之间的关系近似满足一次函数:
之间的关系近似满足一次函数:![]() 已知这种节能灯批发价为每件12元,设它的生产成本价为每件m元
已知这种节能灯批发价为每件12元,设它的生产成本价为每件m元![]()
(1)当![]() 时.
时.
①若第一个月的销售单价定为20元,则第一个月政府要给该企业补偿多少元?
②设所获得的利润为![]() 元
元![]() ,当销售单价定为多少元时,每月可获得最大利润?
,当销售单价定为多少元时,每月可获得最大利润?
(2)物价部门规定,这种节能灯的销售单价不得超过30元![]() 今年三月小明获得赢利,此时政府给该企业补偿了920元,若m,x都是正整数,求m的值.
今年三月小明获得赢利,此时政府给该企业补偿了920元,若m,x都是正整数,求m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,AB⊥AC,点E是BC的中点,AE与BD交于点F,且F是AE的中点.
(Ⅰ)求证:四边形AECD是菱形;(Ⅱ)若AC=4,AB=5,求四边形ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com