
科目: 来源: 题型:
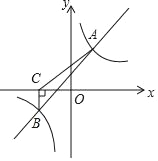
【题目】如图所示,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(2,4),B(﹣4,n)两点.
的图象交于A(2,4),B(﹣4,n)两点.
(1)分别求出一次函数与反比例函数的表达式;
(2)过点B作BC⊥x轴,垂足为点C,连接AC,求△ACB的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图:在平行四边形ABCD的边AB,CD上截取AF,CE,使得AF=CE,连接EF,点M,N是线段EF上两点,且EM=FN,连接AN,CM.
(1)求证:△AFN≌△CEM;
(2)若∠CMF=107°,∠CEM=72°,求∠NAF的度数.

查看答案和解析>>
科目: 来源: 题型:
【题目】“校园手机”现象越来越受到社会的关注.“五一”期间,小记者刘凯随机调查了城区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图:

(1)求这次调查的家长人数,并补全图①;
(2)求图②中表示家长“赞成”的圆心角的度数;
(3)从这次接受调查的学生中,随机抽查一个,恰好是“无所谓”态度的学生的概率是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交DC于点F,连接AF.设![]() =k,下列结论:(1)△ABE∽△ECF,(2)AE平分∠BAF,(3)当k=1时,△ABE∽△ADF,其中结论正确的是( )
=k,下列结论:(1)△ABE∽△ECF,(2)AE平分∠BAF,(3)当k=1时,△ABE∽△ADF,其中结论正确的是( )
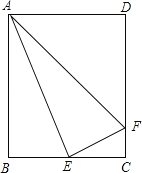
A.(1)(2)(3) B.(1)(3) C.(1)(2) D.(2)(3)
查看答案和解析>>
科目: 来源: 题型:
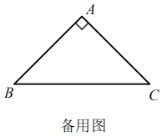
【题目】在RtΔABC中,∠BAC=90°,点O是△ABC所在平面内一点,连接OA,延长OA到点E,使得AE=OA,连接OC,过点B作BD与OC平行,并使∠DBC=∠OCB,且BD=OC,连接DE.
(1)如图一,当点O在RtΔABC内部时.

①按题意补全图形;
②猜想DE与BC的数量关系,并证明.
(2)若AB=AC(如图二),且∠OCB=30°,∠OBC=15°,求∠AED的大小.


查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() (m是常数)的顶点为P,直线l:y=x﹣1
(m是常数)的顶点为P,直线l:y=x﹣1
(1)求证:点P在直线l上;
(2)当m=﹣3时,抛物线与x轴交于A,B两点,与y轴交于点C,与直线l的另一个交点为Q,M是x轴下方抛物线上的一点,∠ACM=∠PAQ(如图),求点M的坐标;
(3)若以抛物线和直线l的两个交点及坐标原点为顶点的三角形是等腰三角形,请直接写出所有符合条件的m的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.

(1)BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1、E1、E2、C2、E3、E4、…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3∥…,则正方形A2018B2018C2018D2018的边长是_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的是( )
①用两颗钉子就可以把木条固定在墙上;②把笔尖看成一个点,当这个点运动时便得到一条线;③把弯曲的公路改直,就能缩短路程;④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com