
科目: 来源: 题型:
【题目】701班小强买了张100元的深圳通乘车卡,如果他乘车的次数用![]() 表示,则记录他每次乘车后的余额n (元)如下表:
表示,则记录他每次乘车后的余额n (元)如下表:
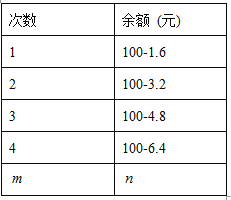
(1)写出余额n与乘车的次数m的关系式.
(2)利用上述关系式计算小强乘了23次车还剩下多少元?
(3)小强最多能乘几次车?
查看答案和解析>>
科目: 来源: 题型:
【题目】某运输公司承担了某标段的土方运输任务,公司已派出大小两种型号的渣土运输车运输土方,已知2辆大型渣土运输车与3辆小型渣土运输车每次共35吨,3辆大型渣土运输车和2辆小型渣土运输车每次共运40吨.
(1)一辆大型渣土运输车和一辆小型渣土运输车每次各运土方多少吨?
(2)该运输公司决定派出大小两种型号的渣土运输车共20辆参与运输土方,若每次运输土方总量不小于150吨,问该运输公司最多派出几辆小型渣土运输车?
查看答案和解析>>
科目: 来源: 题型:
【题目】问题情填,
在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动,如图1,将矩形纸片ABCD沿对角线AC剪开,得到△ABC和△ACD、并且量得AB=2cm,AC=4cm.
操作发现:
(1)将图1中的△ACD以点A为旋转中心,按逆时针方向旋转∠α,使∠α=∠BAC,得到加图2所示的△AC′D,过点C作AC′的平行线,与DC′的延长线交于点E,则四边形ACEC'的形状是_________;
(2)创新小组将图1中的△ACD以点A为旋转中心,按逆时针方向旋转,使B,A,D三点在同一条直线上,得到如图3所示的△AC′D,连接CC′,取CC'的中点F,连精AF并延长到点G,使FG=AF,连接CG,C′G,得到四边形ACGC′,发现它是正方形,请你证明这个结论.
实践探究:
(3)缜密小组在创新小组发现结论的基础上,进行如下操作:将△ABC沿着BD方向平移,使点B与点A重合,此时A点平移至A′点,A′C与BC′相交于点H.如图4所示,连接CC',试求CH的长度.
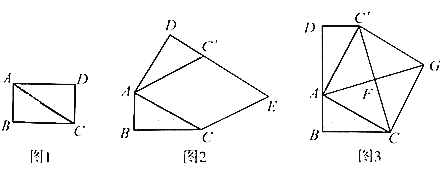
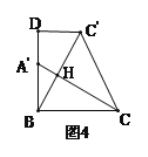
查看答案和解析>>
科目: 来源: 题型:
【题目】回答下列问题:
(1)如图所示的甲、乙两个平面图形能折什么几何体?
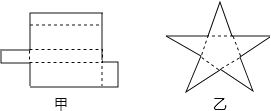
(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点个数为v,棱数为e,分别计算第(1)题中两个多面体的f+v﹣e的值?你发现什么规律?
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
1 | ° | x | 7 | ﹣3 | … |
(1)可知x= ,= ,°= ;
(2)试判断第2016个格子中的数是多少?并给出相应的理由.
(3)判断:前n个格子中所填整数之和是否可能为2016?若能,求出n的值,若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点E在菱形ABCD的对角线BD上,连接AE,且AE=BE,⊙O是△ABE的外接圆,连接OB.
(1)求证:OB⊥BC;
(2)若BD=![]() ,tan∠OBD=2,求⊙O的半径.
,tan∠OBD=2,求⊙O的半径.
查看答案和解析>>
科目: 来源: 题型:
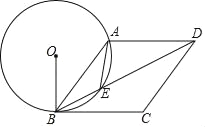
【题目】(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE="10," 求直角梯形ABCD的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某报社为了解市民对“社会主义核心价值观”的知晓程度,采取随机抽样的方式进行问题卷调查,调查结果分为“A非常了解”、“B了解”、“C基本了解”三个等级,并根据调查结果制作了如下两幅不完整的统计图.
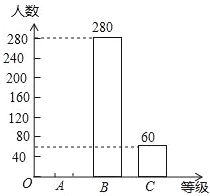
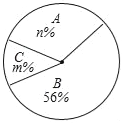
(1)这次调查的市民有多少人?
(2)补全条形统计图;
(2)若该市约有市民950万人,请你根据抽样调查的结果,估计该市有多少万人对“社会主义核心价值观”达到“A非常了解”的程度.
查看答案和解析>>
科目: 来源: 题型:
【题目】仔细阅读下面例题,解答问题:
例题:已知二次三项式x2-4x+m有一个因式是(x+3),求另一个因式以及m的值.
解:设另一个因式为(x+n),得x2-4x+m=(x+3)(x+n),则x2-4x+m=x2+(n+3)x+3n.
∴![]() ,
,
解得:![]() .
.
∴另一个因式为(x-7),m的值为-21.
问题:仿照以上方法解答下面问题:
(1)已知二次三项式2x2+3x-k有一个因式是(2x-5),求另一个因式以及k的值
(2)已知二次三项式6x2+4ax+2有一个因式是(2x+a),a是正整数,求另一个因式以及a的值.
查看答案和解析>>
科目: 来源: 题型:
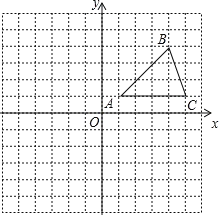
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形)。
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标;
(3)在第(2)问中,点B旋转到点B2的过程中运动的路径长是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com