
科目: 来源: 题型:
【题目】直接填答案:
①(-5)+(-5)=______;②(-5)+(+8)=______;③90![]() (-3)=______;
(-3)=______;
④(-5)-(-3)=______;⑤-16-8=_____;⑥8-16=______;
⑦![]() =______;⑧
=______;⑧![]() =_____。
=_____。
⑨ ![]() =_____;⑩
=_____;⑩![]() =______。
=______。
查看答案和解析>>
科目: 来源: 题型:
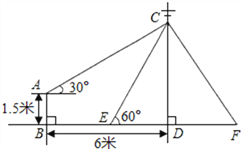
【题目】如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角
∠CED=60°,在离电线杆6米的B处安置测角仪AB,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长 (结果精确到0.1米,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732).
≈1.732).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在公路 MN 两侧分别有 A![]() , A
, A![]() ......A
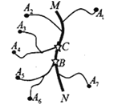
......A![]() ,七个工厂,各工厂与公路 MN(图中粗线)之间有小公路连接.现在需要在公路 MN 上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是( ).
,七个工厂,各工厂与公路 MN(图中粗线)之间有小公路连接.现在需要在公路 MN 上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是( ).
①车站的位置设在 C 点好于 B 点;
②车站的位置设在 B 点与 C 点之问公路上任何一点效果一样;
③车站位置的设置与各段小公路的长度无关.
A.①B.②C.①③D.②③
查看答案和解析>>
科目: 来源: 题型:
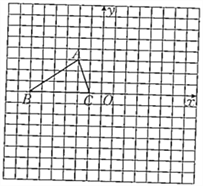
【题目】如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
(1)画出将△ABC绕坐标原点O逆时针旋转90°图形.
(2)填空:以A、B、C为顶点的平行四边形的第四个顶点D的坐标为________.
查看答案和解析>>
科目: 来源: 题型:
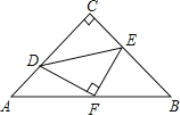
【题目】如图,已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD,FE分别交AC,BC于点D,E两点,当∠DFE在△ABC内绕顶点F旋转时(点D不与A,C重合),给出以下个结论:①CD=BE;②四边形CDFE不可能是正方形;③△DFE是等腰直角三角形;④S四边形CDFE=![]() S△ABC.上述结论中始终正确的有______.(填序号)
S△ABC.上述结论中始终正确的有______.(填序号)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一条公路的转弯处是一段圆弧(![]() ).
).
(1)用直尺和圆规作出![]() 所在圆的圆心
所在圆的圆心![]() ;(要求保留作图痕迹,不写作法)
;(要求保留作图痕迹,不写作法)
(2)若![]() 的中点
的中点![]() 到
到![]() 的距离为
的距离为![]() m,
m,![]() m,求
m,求![]() 所在圆的半径.
所在圆的半径.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣![]() ),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求m的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】观察下表:

我们把表格中字母的和所得的多项式称为"'特征多项式",例如:第1格的“特征多项式”为 4x+y,第 2 格的“特征多项式”为 8x+4y, 回答下列问题:
(1)第 3 格的“特征多项式”为 第 4 格的“待征多项式”为 , 第 n 格的“特征多项式”为 .
(2)若第 m 格的“特征多项式”与多项式-24x+2y-5 的和不含有 x 项,求此“特征多项式”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com