【题目】如图，点，分别在直线和上，若，，可以证明.请完成下面证明过程中的各项“填空”.

证明：∵（理由：______.）

______（对顶角相等）

∴，∴（理由：______）

∴______（两直线平行，同位角相等）

又∵，∴，

∴______（内错角相等，两直线平行）

∴（理由：______）

【题目】如图，已知，，试说明直线AD与BC垂直请在下面的解答过程的空格内填空或在括号内填写理由．

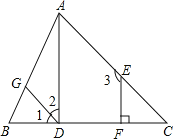
理由：，已知

____________，______

____________

又，已知

______等量代换

____________，______

______

，已知

，，

____________．

【题目】抛物线y=ax2+bx+3（a≠0）经过点A（﹣1，0），B（，0），且与y轴相交于点C．

（1）求这条抛物线的表达式；

（2）求∠ACB的度数；

（3）设点D是所求抛物线第一象限上一点，且在对称轴的右侧，点E在线段AC上，且DE⊥AC，当△DCE与△AOC相似时，求点D的坐标．

（1）如果七年级一班代表队最后得分为190分，那么七年级一班代表队回答对了多少道题？

（2）七年级二班代表队的最后得分有可能为142分吗？请说明理由．

(1)试判断DG与BC的位置关系，并说明理由．

(2)若∠A＝70°，∠B＝40°，求∠AGD的度数．

【题目】两条直线被第三条直线所截，就第三条直线上的两个交点而言形成了“三线八角”为了便于记忆，同学们可仿照图用双手表示“三线八角”两大拇指代表被截直线，食指代表截线下列三幅图依次表示　　

A. 同位角、同旁内角、内错角B. 同位角、内错角、同旁内角

C. 同位角、对顶角、同旁内角D. 同位角、内错角、对顶角

根据以上信息解答下列问题：

（1）m=　 　，n=　 　，p=　 　．

（2）求本次参与调查的总人数，并补全条形统计图．

（3）若该中学约有800名学生，估计全校学生中利用手机购物或玩游戏的共有多少人？并根据以上调查结果，就中学生如何合理使用手机给出你的一条建议．

（1）求直线AB和反比例函数的解析式；

（2）观察图象，直接写出当x满足什么范围时，直线AB在双曲线的下方；

（3）反比例函数的图象上是否存在点C，使得△OBC的面积等于△OAB的面积？如果不存在，说明理由；如果存在，求出满足条件的所有点C的坐标．

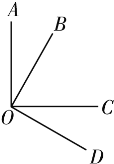
(1)若∠BOC＝35°，则∠AOB= ，∠COD= ;

(2)若∠BOC＝46°，则∠AOB= ，∠COD= .

(3)你发现了什么？你能说明其中的道理吗？

(1)若∠AOC=则∠BOC=_______，∠AOM=_______，∠BON=_________；

(2)若∠AOC=则∠BON=_______(用含有的式子表示)；

(3)将∠AOB绕着点O顺时针转到图2的位置,其他条件不变，若∠AOC=(为钝角),求∠BON的度数(用含的式子表示).