
科目: 来源: 题型:
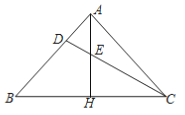
【题目】如图,AH是△ABC的高,D是边AB上一点,CD与AH交于点E.已知AB=AC=6,cosB=![]() ,
,
AD∶DB=1∶2.
(1)求△ABC的面积;
(2)求CE∶DE.
查看答案和解析>>
科目: 来源: 题型:
【题目】如下图,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环下去.
(1)填写下表:
剪的次数 | 1 | 2 | 3 | 4 | 5 |
正方形个数 | 4 | 7 | 10 |
|
|
(2)如果剪了8次,共剪出 个小正方形.
(3)如果剪n次,共剪出 个小正方形.
(4)设最初正方形纸片为1,则剪n次后,最小正方形的边长为 .

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,反比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于点
的图像交于点![]() ,点
,点![]() 的横坐标是
的横坐标是![]() ,点
,点![]() 是第一象限内反比例函数图像上的动点,且在直线
是第一象限内反比例函数图像上的动点,且在直线![]() 的上方.
的上方.
(1)若点![]() 的坐标是
的坐标是![]() ,则
,则![]() ,
,![]() ;
;
(2)设直线![]() 与
与![]() 轴分别交于
轴分别交于![]() 点,求证:
点,求证:![]() 是等腰三角形;
是等腰三角形;
(3)设点![]() 是反比例函数图像位于
是反比例函数图像位于![]() 之间的动点(与点
之间的动点(与点![]() 不重合),连接
不重合),连接![]() ,比较
,比较![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】在一张足够大的纸板上截取一个面积为![]() 的矩形纸板
的矩形纸板![]() ,如图
,如图![]() ,再在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒,底面
,再在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒,底面![]() 为矩形,如图
为矩形,如图![]() ,设小正方形的边长为
,设小正方形的边长为![]() 厘米.、
厘米.、
(1)若矩形纸板的一个边长为![]() .
.
①当纸盒的底面积为![]() 时,求
时,求![]() 的值;
的值;
②求纸盒的侧面积的最大值;
(2)当![]() ,且侧面积与底面积之比为
,且侧面积与底面积之比为![]() 时,求
时,求![]() 的值.
的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】用小立方块搭成的几何体.从正面看和从上面看的形状如图所示,问组成这样的几何体最多需要多少个立方块,最少需要多少个立方块?请画出最少和最多时从左面看到的形状.

查看答案和解析>>
科目: 来源: 题型:
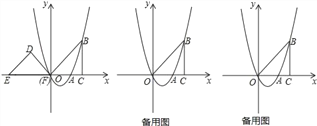
【题目】如图,抛物线y=ax2+bx(a≠0)经过点A(2,0),点B(3,3),BC⊥x轴于点C,连接OB,等腰直角三角形DEF的斜边EF在x轴上,点E的坐标为(﹣4,0),点F与原点重合
(1)求抛物线的解析式并直接写出它的对称轴;
(2)△DEF以每秒1个单位长度的速度沿x轴正方向移动,运动时间为t秒,当点D落在BC边上时停止运动,设△DEF与△OBC的重叠部分的面积为S,求出S关于t的函数关系式;
(3)点P是抛物线对称轴上一点,当△ABP是直角三角形时,请直接写出所有符合条件的点P坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为了迎接体育中考,了解学生的体质情况,学校随机调查了本校九年级![]() 名学生“
名学生“![]() 秒跳绳”的次数,并将调查所得的数据整理如下:
秒跳绳”的次数,并将调查所得的数据整理如下:
![]() 秒跳绳次数的频数、频率分布表
秒跳绳次数的频数、频率分布表
![]() 秒跳绳次数的频数分布直方图
秒跳绳次数的频数分布直方图
 、
、
根据以上信息,解答下列问题:
(1)表中,![]() ,
,![]() ;
;
(2)请把频数分布直方图补充完整;
(3)若该校九年级共有![]() 名学生,请你估计“
名学生,请你估计“![]() 秒跳绳”的次数
秒跳绳”的次数![]() 以上(含
以上(含![]() 次)的学生有多少人?
次)的学生有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,用同样规格的黑白两色正方形瓷砖铺设长方形地面,观察下列图形,探究并解答问题:
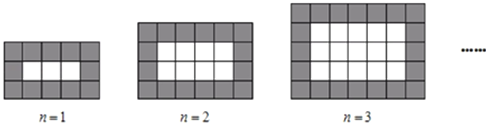
(1)在第4个图中,共有白色瓷砖______块;在第![]() 个图中,共有白色瓷砖_____块;
个图中,共有白色瓷砖_____块;
(2)试用含![]() 的代数式表示在第
的代数式表示在第![]() 个图中共有瓷砖的块数;
个图中共有瓷砖的块数;
(3)如果每块黑瓷砖35元,每块白瓷砖50元,当![]() 时,求铺设长方形地面共需花多少钱购买瓷砖?
时,求铺设长方形地面共需花多少钱购买瓷砖?
查看答案和解析>>
科目: 来源: 题型:
【题目】“十一”期间,某风景区在7天中每天游客的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
人数变化 单位:万人 |
|
|
|
|
|
|
|
(1)若9月30日的游客人数记为![]() ,请用含
,请用含![]() 的代数式表示10月2日的游客人数?
的代数式表示10月2日的游客人数?
(2)请判断七天内游客人数最多的是哪天?请说明理由.
(3)此风景区一方面给广大市民提供一个休闲游玩的好去处;另一方面拉动了内需,促进了消费.若9月30日的游客人数为1万人,进园的人每人平均消费60元,问“十一”期间所有游园人员在此风景区的总消费是多少元?(用科学记数法表示)
查看答案和解析>>
科目: 来源: 题型:
【题目】在平整的地面上,由若干个完全相同的棱长为 10 cm 的小正方体堆成一个几何体,如图 所示.
(1)这个几何体由多少个小正方体组成?请画出这个几何体的三视图.
(2)如果在这个几何体的表面(不包括底面)喷上黄色的漆,则在所有的小正方体中,有多少个只有一个面是黄色?有多少个只有两个面是黄色?有多少个只有三个面是黄色?
(3)假设现在你手里还有一些相同的小正方体,保持这个几何体的主视图、俯视图形状 不变,最多可以再添加几个小正方体?这时如果要重新给这个几何体表面(不包括底面) 喷上红色的漆,需要喷漆的面积比原几何体增加了还是减少了?增加或减少的面积是 多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com