
科目: 来源: 题型:
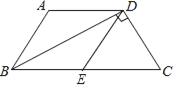
【题目】已知:如图,四边形ABCD中,AD∥BC,对角线BD平分∠ABC,且BD⊥DC,E为BC中点,AB=DE.
(1)求证:四边形ABED是菱形;
(2)若∠C=60°,CD=4,求四边形ABCD的面积.
查看答案和解析>>
科目: 来源: 题型:
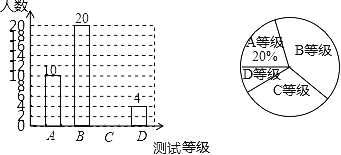
【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.
【答案】(1)50;(2)16;(3)56(4)见解析
【解析】试题分析:
(1)根据统计图中的信息可知,获得A等的有10人,占抽查总数的20%,由此即可计算出抽查学生的总数;
(2)由(1)中计算结果结合统计图中已知的A、B、D三个等级的人数即可求得C等级的人数,并由此补全条形统计图;
(3)由(1)中求得的被抽查学生的总数及获得D等级的有4人可计算出获得D等级的人数所占的百分比,即可求得800人中可能获得D等级的人数;
(4)设两名男生为A1、A2,两名女生为B1、B2,画出树形图分析即可求得所求概率;
试题解析:
(1)10÷20%=50(名)
答:本次抽样调查共抽取了50名学生.
(2)50-10-20-4=16(名)
答:测试结果为C等级的学生有16名.
图形统计图补充完整如下图所示:
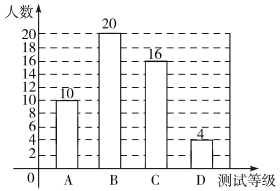
(3)700×![]() =56(名)
=56(名)
答:估计该中学八年级学生中体能测试结果为D等级的学生有56名.
(4)画树状图法:设体能为A等级的两名男生分别为![]() ,体能为A等级的两名女生分别为
,体能为A等级的两名女生分别为![]() ,
,![]() ,画树状图如下:
,画树状图如下:
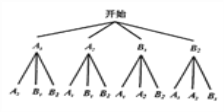
由树状图可知,共有12 种结果,每种结果出现的可能性相同,而抽取的两人都是男生的结果有两种:(![]() ),(
),(![]() ,
,![]() ), ∴P(抽取的两人是男生)=
), ∴P(抽取的两人是男生)=![]() .
.
【题型】解答题
【结束】
20
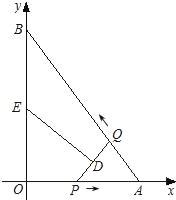
【题目】如图,在平面直角坐标系xOy中,直线AB与x轴交于点A,与y轴交于点B,且OA=3,AB=5.点P从点O出发沿OA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AO返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB﹣BO﹣OP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0).
(1)求直线AB的解析式;
(2)在点P从O向A运动的过程中,求△APQ的面积S与t之间的函数关系式(不必写出t的取值范围);
(3)在点E从B向O运动的过程中,完成下面问题:
①四边形QBED能否成为直角梯形?若能,请求出t的值;若不能,请说明理由;
②当DE经过点O时,请你直接写出t的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】(2011贵州安顺,17,4分)已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为 .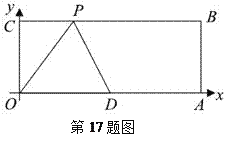
查看答案和解析>>
科目: 来源: 题型:
【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.

查看答案和解析>>
科目: 来源: 题型:
【题目】下列结论:①若![]() ,则关于x的方程 ax-b+c=0(a
,则关于x的方程 ax-b+c=0(a![]() 的解是x=-1;②若x=1是方程ax+b+c=1且a
的解是x=-1;②若x=1是方程ax+b+c=1且a![]() 的解,则a+b+c=1成立;③若
的解,则a+b+c=1成立;③若![]() ,则
,则![]() ;④A、B、C是平面内的三个点,AB与AC是两条线段,若AB=AC,则点C为线段AB的中点;⑤若
;④A、B、C是平面内的三个点,AB与AC是两条线段,若AB=AC,则点C为线段AB的中点;⑤若![]() ,则
,则![]() 的值为0。其中正确结论的个数是( )
的值为0。其中正确结论的个数是( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目: 来源: 题型:
【题目】等边三角形(三条边都相等的三角形是等边三角形)纸板ABC在数轴上的位置如图所示,点A,B对应的数分别为0和-1,若⊿ABC绕着顶点顺时针方向在数轴上连续翻转,翻转第1次后,点C所对应的数为1,则翻转2020次后,点C所对应的数是( )

A.2017B.2018C.2019D.2020
查看答案和解析>>
科目: 来源: 题型:
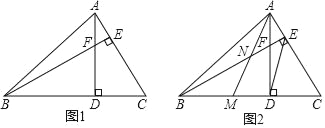
【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.
【答案】(1)BF=AC,理由见解析;(2)NE=![]() AC,理由见解析.
AC,理由见解析.
【解析】试题分析:(1)如图1,证明△ADC≌△BDF(AAS),可得BF=AC;
(2)如图2,由折叠得:MD=DC,先根据三角形中位线的推论可得:AE=EC,由线段垂直平分线的性质得:AB=BC,则∠ABE=∠CBE,结合(1)得:△BDF≌△ADM,则∠DBF=∠MAD,最后证明∠ANE=∠NAE=45°,得AE=EN,所以EN=![]() AC.
AC.
试题解析:
(1)BF=AC,理由是:
如图1,∵AD⊥BC,BE⊥AC,
∴∠ADB=∠AEF=90°,
∵∠ABC=45°,
∴△ABD是等腰直角三角形,
∴AD=BD,
∵∠AFE=∠BFD,
∴∠DAC=∠EBC,
在△ADC和△BDF中,
∵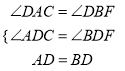 ,
,
∴△ADC≌△BDF(AAS),
∴BF=AC;
(2)NE=![]() AC,理由是:
AC,理由是:
如图2,由折叠得:MD=DC,
∵DE∥AM,
∴AE=EC,
∵BE⊥AC,
∴AB=BC,
∴∠ABE=∠CBE,
由(1)得:△ADC≌△BDF,
∵△ADC≌△ADM,
∴△BDF≌△ADM,
∴∠DBF=∠MAD,
∵∠DBA=∠BAD=45°,
∴∠DBA﹣∠DBF=∠BAD﹣∠MAD,
即∠ABE=∠BAN,
∵∠ANE=∠ABE+∠BAN=2∠ABE,
∠NAE=2∠NAD=2∠CBE,
∴∠ANE=∠NAE=45°,
∴AE=EN,
∴EN=![]() AC.
AC.
【题型】解答题
【结束】
17
【题目】已知x1,x2是方程2x2﹣2nx+![]() n(n+4)=0的两根,且(x1﹣1)(x2﹣1)﹣1=
n(n+4)=0的两根,且(x1﹣1)(x2﹣1)﹣1=![]() ,求n的值.
,求n的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点A、B在数轴上分别表示a,b.请认真观察数轴及表格再解答问题:
![]()

(1)表格中的m=_____,n=________
(2)若A、B两点间的距离记为d,则d与a、b间的等量关系为__________
(3)结合上述结论,并利用数轴解答下列问题
①满足到表示数4和-6的点的距离之和等于16的数为
②若点C表示的数为x,求![]() 的最小值.(本页可作为草稿纸使用)
的最小值.(本页可作为草稿纸使用)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线m∥n,直线l与m、n分别相交于点A和点C,AC为对角线作四边形ABCD,使点B和点D分别在直线m和n上,则不能作出的图形是( )
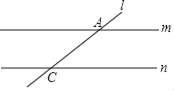
A. 平行四边形ABCDB. 矩形ABCD
C. 菱形ABCDD. 正方形ABCD
查看答案和解析>>
科目: 来源: 题型:
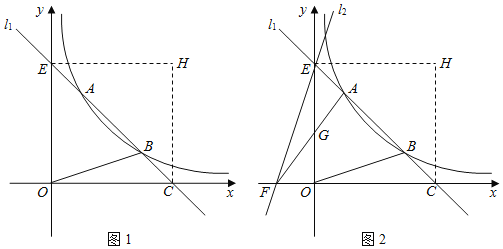
【题目】如图1,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() 、点
、点![]() .
.
(1)求直线![]() 和双曲线的解析式;
和双曲线的解析式;
(2)将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在第一象限内的点
落在第一象限内的点![]() 处,直接写出点
处,直接写出点![]() 的坐标;
的坐标;
(3)如图2,过点![]() 作直线
作直线![]() 交
交![]() 轴的负半轴于点
轴的负半轴于点![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() 的面积与
的面积与![]() 的面积相等.
的面积相等.
①求直线![]() 的解析式;
的解析式;
②在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,请直接写出所有符合条件的点
?若存在,请直接写出所有符合条件的点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com