
科目: 来源: 题型:
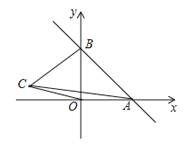
【题目】如图,一次函数y=kx+b的图象分别与x轴,y轴的正半轴分別交于点A,B,AB=2![]() ,∠OAB=45°
,∠OAB=45°
(1)求一次函数的解析式;
(2)如果在第二象限内有一点C(a,![]() );试用含有a的代数式表示四边形ABCO的面积,并求出当△ABC的面积与△ABO的面积相等时a的值;
);试用含有a的代数式表示四边形ABCO的面积,并求出当△ABC的面积与△ABO的面积相等时a的值;
(3)在x轴上,是否存在点P,使△PAB为等腰三角形?若存在,请直接写出所有符合条件的点P坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】完成下列推理,并填写完理由
已知,如图,∠BAE+∠AED=180°,∠M=∠N,
试说明:![]()
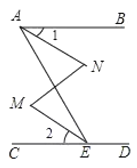
解:∵∠BAE+∠AED=180(已知)
∴ ∥ ( )
∴∠BAE= ( 两直线平行,内错角相等 )
又∵∠M=∠N (已知)
∴ ∥ ( )
∴∠NAE= ( )
∴∠BAE-∠NAE= - ( )
即∠1=∠2
查看答案和解析>>
科目: 来源: 题型:
【题目】今年水果大丰收,A,B两个水果基地分别收获水果380件、320件,现需把这些水果全部运往甲、乙两销售点,从A基地运往甲、乙两销售点的费用分别为每件40元和20元,从B基地运往甲、乙两销售点的费用分别为每件15元和30元,现甲销售点需要水果400件,乙销售点需要水果300件.
(1)设从A基地运往甲销售点水果x件,总运费为W元,请用含x的代数式表示W,并写出x的取值范围;
(2)若总运费不超过18300元,且A地运往甲销售点的水果不低于200件,试确定运费最低的运输方案,并求出最低运费.
查看答案和解析>>
科目: 来源: 题型:
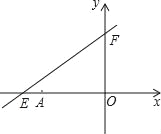
【题目】如图,直线y=kx+6分别与x轴、y轴交于点E,F,已知点E的坐标为(﹣8,0),点A的坐标为(﹣6,0).
(1)求k的值;
(2)若点P(x,y)是该直线上的一个动点,且在第二象限内运动,试写出△OPA的面积S关于x的函数解析式,并写出自变量x的取值范围.
(3)探究:当点P运动到什么位置时,△OPA的面积为![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】仙居吾悦广场于![]() 年
年![]() 月
月![]() 日开业,商场内两家服装店举行开业大酬宾活动,甲乙两家服装店优惠活动如下表:
日开业,商场内两家服装店举行开业大酬宾活动,甲乙两家服装店优惠活动如下表:
购买服装总金额(元) | 不超过 | 超过 |
|
优惠幅度 | 打 | 打 | 打 |
乙服装店优惠活动:购买服装总金额每满![]() 元减
元减![]() 元.
元.
例如:购买总金额满![]() 元减
元减![]() 元,满
元,满![]() 元减
元减![]() 元,以此类推.
元,以此类推.
(1)若在两家店购买服装总金额都是![]() 元,哪家店实际付款更少?少多少?
元,哪家店实际付款更少?少多少?
(2)若购买服装总金额小于![]() 元,选择哪家店购买服装更划算?请通过计算说明理由.
元,选择哪家店购买服装更划算?请通过计算说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.

查看答案和解析>>
科目: 来源: 题型:
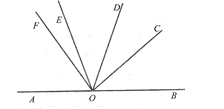
【题目】如图,点![]() ,
,![]() ,
,![]() 在同一直线上,射线
在同一直线上,射线![]() 在
在![]() 的内部,
的内部,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的平分线,请探究
的平分线,请探究![]() 与
与![]() 的数量关系.
的数量关系.
(1)当![]() ,
,![]() 时,求出
时,求出![]() 和
和![]() 的度数,并写出他们的数量关系;
的度数,并写出他们的数量关系;
(2)一般情况下,写出![]() 和
和![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,我们把任意形如:![]() 的五位自然数(其中
的五位自然数(其中![]() ,
,![]() ,
,![]() )称之为喜马拉雅数,例如:在自然数
)称之为喜马拉雅数,例如:在自然数![]() 中,
中,![]() ,所以
,所以![]() 就是一个喜马拉雅数.并规定:能被自然数
就是一个喜马拉雅数.并规定:能被自然数![]() 整除的最大的喜马拉雅数记为
整除的最大的喜马拉雅数记为![]() ,能被自然数
,能被自然数![]() 整除的最小的喜马拉雅数记为
整除的最小的喜马拉雅数记为![]() .
.
(1)求证:任意一个喜马拉雅数都能被3整除;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,点
,点![]() 为边
为边![]() 上一点,连接
上一点,连接![]() 交对角线
交对角线![]() 于点
于点![]() .
.
(1)如图1,已知![]() 于
于![]() ,菱形的边长为6,求线段
,菱形的边长为6,求线段![]() 的长度;
的长度;
(2)如图2,已知点![]() 为边
为边![]() 上一点,连接
上一点,连接![]() 交线段
交线段![]() 于点
于点![]() ,且满足
,且满足![]() ,
,![]() ,求证:
,求证:![]() .
.
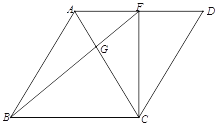
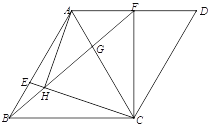
图1 图2
查看答案和解析>>
科目: 来源: 题型:
【题目】每年的3月15日是 “国际消费者权益日”,许多家居商城都会利用这个契机进行打折促销活动.甲卖家的某款沙发每套成本为5000元,在标价8000元的基础上打9折销售.
(1)现在甲卖家欲继续降价吸引买主,问最多降价多少元,才能使利润率不低于20%?
(2)据媒体爆料,有一些卖家先提高商品价格后再降价促销,存在欺诈行为.乙卖家也销售相同的沙发,其成本、标价与甲卖家一致,以前每周可售出5套,现乙卖家先将标价提高m%,再大幅降价40m元,使得这款沙发在3月15日那一天卖出的数量就比原来一周卖出的数量增加了![]() m%,这样一天的利润达到了31250元,求m.
m%,这样一天的利润达到了31250元,求m.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com