
科目: 来源: 题型:
【题目】(1)观察思考:如图,线段AB上有两个点C、D,请分别写出以点A、B、C、D为端点的线段,并计算图中共有多少条线段;
(2)模型构建:如果线段上有m个点(包括线段的两个端点),则该线段上共有多少条线段?请说明你结论的正确性;
(3)拓展应用:某班45名同学在毕业后的一次聚会中,若每两人握1次手问好,那么共握多少次手?
请将这个问题转化为上述模型,并直接应用上述模型的结论解决问题.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,AB是⊙O的直径,弦BC=2cm,∠ABC=60.
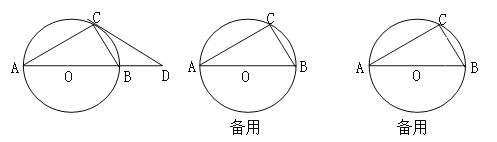
(1)求⊙O的直径;
(2)若D是AB延长线上一点,连结CD,当BD长为多少时,CD与⊙O相切;
(3)若动点E以2cm/s的速度从点A出发沿着AB方向运动,同时动点F以1cm/s的速度从点B出发沿BC方向运动,设运动时间为t(s)(0<t<2),连结EF,当t为何值时,△BEF为直角三角形.
查看答案和解析>>
科目: 来源: 题型:
【题目】某星期六上午,小明从家出发跑步去公园,在公园停留了一会儿打车回家.图中折线表 示小明离开家的路程y(米)和所用时间x(分)之间的函数关系,则下列说法中错误的是( )
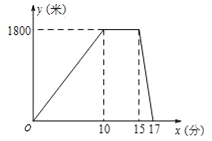
A.小明在公园休息了5分钟
B.小明乘出租车用了17分
C.小明跑步的速度为180米/分
D.出租车的平均速度是900米/分
查看答案和解析>>
科目: 来源: 题型:
【题目】探究:如图1,在△ABC中,AB=AC,CF为AB边上的高,点P为BC边上任意一点,PD⊥AB,PE⊥AC,垂足分别为点D,E.求证:PD+PE=CF.
嘉嘉的证明思路:连结AP,借助△ABP与△ACP的面积和等于△ABC的面积来证明结论.
淇淇的证明思路:过点P作PG⊥CF于G,可证得PD=GF,PE=CG,则PD+PE=CF.
迁移:请参考嘉嘉或淇淇的证明思路,完成下面的问题:
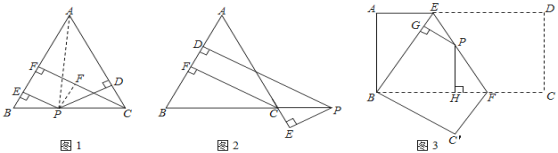
(1)如图2.当点P在BC延长线上时,其余条件不变,上面的结论还成立吗?若不成立,又存在怎样的关系?请说明理由;
(2)当点P在CB延长线上时,其余条件不变,请直接写出线段PD,PE和CF之间的数量关系.
运用:如图3,将矩形ABCD沿EF折叠,使点D落在点B处,点C落在点C′处.若点P为折痕EF上任一点,PG⊥BE于G,PH⊥BC于H,若AD=18,CF=5,直接写出PG+PH的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,A,B,C,D为四家超市,其中超市D距A,B,C三家超市的路程分别为25km,10km,5km.现计划在A,D之间的道路上建一个配货中心P,为避免交通拥堵,配货中心与超市之间的距离不少于2km.假设一辆货车每天从P出发为这四家超市送货各1次,由于货车每次仅能给一家超市送货,因此每次送货后均要返回配货中心P,重新装货后再前往其他超市.设P到A的路程为xkm,这辆货车每天行驶的路程为ykm.
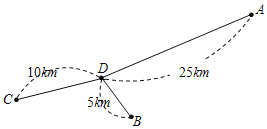
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)直接写出配货中心P建在什么位置,这辆货车每天行驶的路程最短?最短路程是多少?
查看答案和解析>>
科目: 来源: 题型:
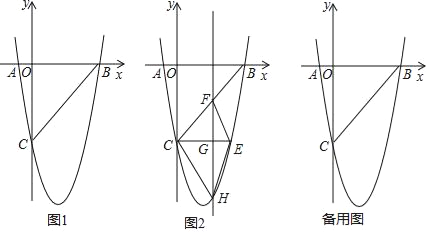
【题目】如图1,在平面直角坐标系中,已知抛物线y=ax2+bx﹣5与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C.
(1)求抛物线的函数表达式;
(2)如图2,CE∥x轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC,CE分别相交于点F,G,试探究当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标;
(3)若点K为抛物线的顶点,点M(4,m)是该抛物线上的一点,在x轴,y轴上分别找点P,Q,使四边形PQKM的周长最小,求出点P,Q的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】∠AOB与∠COD有共同的顶点O,其中∠AOB=∠COD=60°.
(1)如图①,试判断∠AOC与∠BOD的大小关系,并说明理由;
(2)如图①,若∠BOC=10°,求∠AOD的度数;
(3)如图①,猜想∠AOD与∠BOC的数量关系,并说明理由;
(4)若改变∠AOB,∠COD的位置,如图②,则(3)的结论还成立吗?若成立,请证明;若不成立,请直接写出你的猜想.

查看答案和解析>>
科目: 来源: 题型:
【题目】某校八年级的体育老师为了解本年级学生对球类运动的爱好情况,抽取了该年级部分学生对篮球、足球、排球、乒乓球的爱好情况进行了调查,并将调查结果绘制成如图所示的两幅不完整的统计图[说明:每位学生只选一种自己最喜欢的一种球类)请根据这两幅图形解答下列问题:
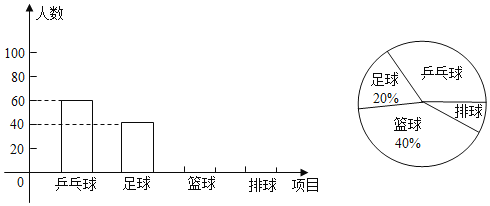
(1)此次被调查的学生总人数为 人.
(2)将条形统计图补充完整,并求出乒乓球在扇形中所占的圆心角的度数;
(3)已知该校有760名学生,请你根据调查结果估计爱好足球和排球的学生共有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】两根木条,一根长20cm,另一根长24cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A. 2cm B. 4cm C. 2cm或22cm D. 4cm或44cm
查看答案和解析>>
科目: 来源: 题型:
【题目】【探索发现】
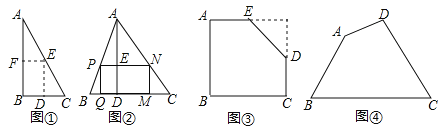
如图①,是一张直角三角形纸片,∠B=60°,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为 .
【拓展应用】
如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为 .(用含a,h的代数式表示)
【灵活应用】
如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.
【实际应用】
如图④,现有一块四边形的木板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=![]() ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com