
科目: 来源: 题型:
【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,如图, 在![]() 中,
中, ![]() ,
,![]() ,
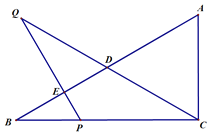
,![]() ,P是边BC上的一动点,过点P作PE⊥AB,垂足为E,延长PE至点Q,使PQ=PC, 联结
,P是边BC上的一动点,过点P作PE⊥AB,垂足为E,延长PE至点Q,使PQ=PC, 联结![]() 交边AB于点
交边AB于点![]() .
.
(1)求AD的长;
(2)设![]() ,
,![]() 的面积为y, 求y关于x的函数解析式,并写出定义域;
的面积为y, 求y关于x的函数解析式,并写出定义域;
(3)过点C作![]() , 垂足为F, 联结PF、QF, 试探索当点P在边BC的什么位置时,
, 垂足为F, 联结PF、QF, 试探索当点P在边BC的什么位置时,![]() 为等边三角形?请指出点P的位置并加以证明.
为等边三角形?请指出点P的位置并加以证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点O为直线AB上一点,过点O作射线OC,将一直角三角板按图中所示的方式摆放(∠MON=900)
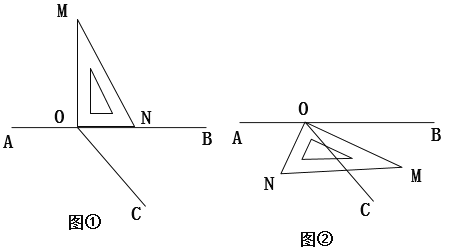
探究一:将图①中的三角板绕点0顺时针方向旋转一定的角度得到图②,使边OM恰好平分∠BOC。若∠BOC=500,ON是否平分∠A0C? 请说明理由;
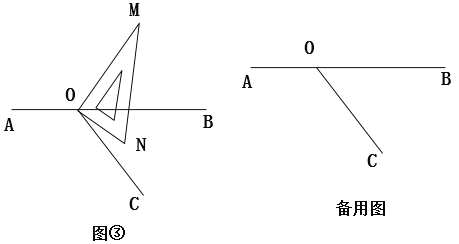
探究二:将图①中的三角板绕点O时针旋转一定的角度得到图③,
(1)使边ON在∠BOC的内部,如果∠BOC=600,则∠BOM与∠CON之间存在怎样的数量关系?请说明理由。
(2)使边ON在∠BOC的内部,则∠BOM与∠NOC之间存在怎样的数量关系?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】课外活动时间,甲、乙、丙、丁4名同学相约进行羽毛球比赛.
(1)如果将4名同学随机分成两组进行对打,求恰好选中甲乙两人对打的概率;
(2)如果确定由丁担任裁判,用“手心、手背”的方法在另三人中竞选两人进行比赛.竞选规则是:三人同时伸出“手心”或“手背”中的一种手势,如果恰好只有两人伸出的手势相同,那么这两人上场,否则重新竞选.这三人伸出“手心”或“手背”都是随机的,求一次竞选就能确定甲、乙进行比赛的概率.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】分析:![]() 列举出将4名同学随机分成两组进行对打所有可能的结果,找出甲乙两人对打的情况数,根据概率公式计算即可.
列举出将4名同学随机分成两组进行对打所有可能的结果,找出甲乙两人对打的情况数,根据概率公式计算即可.
![]() 画树状图写出所有的情况,根据概率的求法计算概率.
画树状图写出所有的情况,根据概率的求法计算概率.
详解:(1)甲同学能和另一个同学对打的情况有三种:
(甲、乙),(甲、丙),(甲、丁)
则恰好选中甲乙两人对打的概率为:![]()
(2)树状图如下:
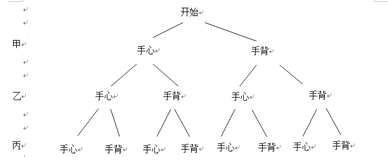
一共有8种等可能的情况,其中能确定甲乙比赛的可能为(手心、手心、手背)、(手背、手背、手心)两种情况,因此,一次竞选就能确定甲、乙进行比赛的概率为![]() .
.
点睛:考查概率的计算,明确概率的意义时解题的关键,概率等于所求情况数与总情况数的比.
【题型】解答题
【结束】
22
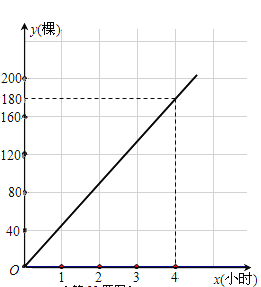
【题目】为了“绿化环境,美化家园”,3月12日(植树节)上午8点,某校901、902班同学同时参加义务植树.901班同学始终以同一速度种植树苗,种植树苗的棵数y1与种植时间x(小时)的函数图象如图所示;902班同学开始以1小时种植40棵的速度工作了1.5小时后,因需更换工具而停下休息半小时,更换工具后种植速度提高至原来的1.5倍.
(1)求902班同学上午11点时种植的树苗棵数;
(2)分别求出901班种植数量y1、902班种植数量y2与种植时间x(小时)之间的函数关系式,并在所给坐标系上画出y2关于x的函数图象;
(3)已知购买树苗不多于120棵时,每棵树苗的价格是20元;购买树苗超过120棵时,超过的部分每棵价格17元.若本次植树所购树苗的平均成本是18元,则两班同学上午几点可以共同完成本次植树任务?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图, l1∥l2,∠1 = 105°,∠2 = 140°,则∠α = _____________.
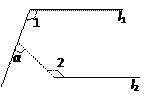
【答案】65°
【解析】分析:反向延长CD交AE于点F,根据平行线的性质得到![]() 根据三角形外角的性质得到
根据三角形外角的性质得到![]() 即可求出.
即可求出.
详解:如图:反向延长CD交AE于点F,
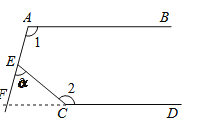
∵AB∥CD,![]()
∴![]()
∵![]()
∴![]()
故答案为:![]()
点睛:考查平行线的性质和三角形外角的性质,解题的关键是作出辅助线.
【题型】填空题
【结束】
14
【题目】如图,AD是⊙O的直径,AD=12,点B、C在⊙O上,AB、DC的延长线交于点E,且CB=CE,∠BCE=70°.
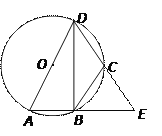
有以下结论:①∠ADE=∠E;②劣弧![]() 的长为
的长为![]() ;③点C为
;③点C为![]() 的中点;④BD平分∠ADE.以上结论一定正确的是_________________.(把正确结论的序号都填上)
的中点;④BD平分∠ADE.以上结论一定正确的是_________________.(把正确结论的序号都填上)
查看答案和解析>>
科目: 来源: 题型:
【题目】2017年11月9日,微信团队在成都腾讯全球合作伙伴大会上发布消息称:2017年全球平均日登录微信用户数9.02亿,较去年增长17%.按此增长速度,预计2019年全球平均日登录微信用户数为( )
A. 9.02×(17%)2亿 B. 9.02×(1+17%)亿 C. 9.02×(1+17%)2亿 D. 9.02×(1+2×17%)亿
查看答案和解析>>
科目: 来源: 题型:
【题目】对于反比例函数![]() ,下列说法不正确的是( )
,下列说法不正确的是( )
A. 点(-2,-1)在它的图像上 B. 它的图像在第一、三象限
C. 当![]() 时,y随x的增大而增大 D. 当
时,y随x的增大而增大 D. 当![]() 时,y随x的增大而减小
时,y随x的增大而减小
【答案】C
【解析】试题分析:反比例函数![]() 的性质:当
的性质:当![]() 时,图象在一、三象限,在每一象限,y随x的增大而减小;当
时,图象在一、三象限,在每一象限,y随x的增大而减小;当![]() 时,图象在二、四象限,在每一象限,y随x的增大而增大.
时,图象在二、四象限,在每一象限,y随x的增大而增大.
A.点![]() 在它的图象上,B.它的图象在第一、三象限,C.当
在它的图象上,B.它的图象在第一、三象限,C.当![]() 时,
时,![]() 随
随![]() 的增大而减小,均正确,不符合题意;
的增大而减小,均正确,不符合题意;
D.当![]() 时,
时,![]() 随
随![]() 的增大而减小,故错误,本选项符合题意.
的增大而减小,故错误,本选项符合题意.
考点:反比例函数的性质
点评:本题属于基础应用题,只需学生熟练掌握反比例函数的性质,即可完成.
【题型】单选题
【结束】
8
【题目】由于各地雾霾天气越来越严重,2018年春节前夕,安庆市政府号召市民,禁放烟花炮竹.学校向3000名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:使用电子鞭炮;D类:不会减少烟花爆竹数量”四个选项进行问卷调查(单选),并将对100名学生的调查结果绘制成统计图(如图所示).根据抽样结果,请估计全校“使用电子鞭炮”的学生有( )
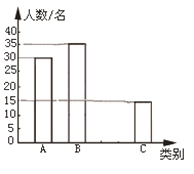
A. 900名 B. 1050名 C. 600名 D. 450名
查看答案和解析>>
科目: 来源: 题型:
【题目】某校八年级共有800名学生,准备调查他们对“低碳”知识的了解程度.
(1)在确定调查方式时,团委设计了以下三种方案:
方案一:调查八年级部分女生;
方案二:调查八年级部分男生;
方案三:到八年级每个班去随机调查一定数量的学生.
请问其中最具有代表性的一个方案是_____;
(2)团委采用了最具有代表性的调查方案,并用收集到的数据绘制出两幅不完整的统计图(如图①、图②所示),请你根据图中信息,将两个统计图补充完整;
(3)请你估计该校八年级约有多少名学生比较了解“低碳”知识.
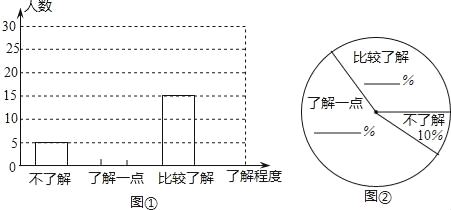
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com