
科目: 来源: 题型:
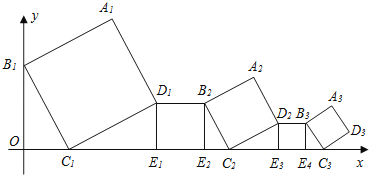
【题目】一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2017B2017C2017D2017的边长是( )
A. (![]() )2016 B. (
)2016 B. (![]() )2017 C. (
)2017 C. (![]() )2016 D. (
)2016 D. (![]() )2017
)2017
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).
ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).

A.AE=CFB.DE=BFC.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
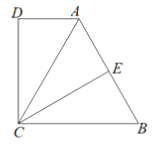
【题目】如图,四边形ABCD中,∠BCD=∠D=90°,E是边AB的中点.已知AD=1,AB=2.
(1)设BC=x,CD=y,求y关于x的函数关系式,并写出定义域;
(2)当∠B=70°时,求∠AEC的度数;
(3)当△ACE为直角三角形时,求边BC的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】在梯形ABCD中,AD∥BC,AB=CD=AD=5cm,BC=11cm,点P从点D开始沿DA边以每秒1cm的速度移动,点Q从点B开始沿BC边以每秒2cm的速度移动(当点P到达点A时,点P与点Q同时停止移动),假设点P移动的时间为x(秒),四边形ABQP的面积为y(cm2).
(1)求y关于x函数解析式,并写出它的定义域;
(2)在移动的过程中,PQ是否可能平分对角线AC?若能,求出x的值;若不能,请说明理由;
(3)在移动的过程中,是否从在x使得PQ=AB,若存在求出所有x的值,若不存在请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】佳乐家超市元旦期间搞促销活动,活动方案如下表:
一次性购物 | 优惠方案 |
不超过200元 | 不给予优惠 |
超过200元,而不超过1000元 | 优惠10% |
超过1000元 | 其中1000元按8.5折优惠,超过部分按7折优惠 |
小颖在促销活动期间两次购物分别支付了134元和913元.
(1)小颖两次购买的物品如果不打折,应支付多少钱?
(2)在此活动中,他节省了多少钱?
查看答案和解析>>
科目: 来源: 题型:
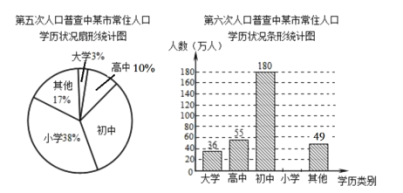
【题目】根据第五次、第六次全国人口普查结果显示:某市常住人口总数由第五次的400万人增加到第六次的450万人,常住人口的学历状况统计图如图所示(部分信息未给出):
解答下列问题:
(1)求第六次人口普查小学学历的人数,并把条形统计图补充完整;
(2)求第五次人口普查中该市常住人口每万人中具有初中学历的人数;
(3)第六次人口普查结果与第五次相比,每万人中初中学历的人数增加了多少人?
查看答案和解析>>
科目: 来源: 题型:
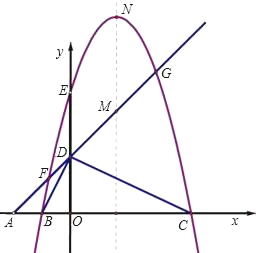
【题目】如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)判断△BDC的形状,并给出证明;当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,并求出此时点P的坐标;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】将图1,将一张直角三角形纸片ABC折叠,使点A与点C重合,这时DE为折痕,△CBE为等腰三角形;再继续将纸片沿△CBE的对称轴EF折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样两个矩形为“叠加矩形”.
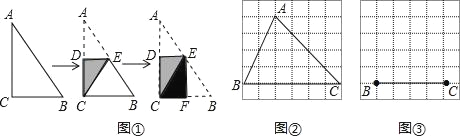
(1)如图2,正方形网格中的△ABC能折叠成“叠加矩形”吗?如果能,请在图2中画出折痕;
(2)如图3,在正方形网格中,以给定的BC为一边,画出一个斜三角形ABC,使其顶点A在格点上,且△ABC折成的“叠加矩形”为正方形;
(3)如果一个三角形所折成的“叠加矩形”为正方形,那么它必须满足的条件是 ;
(4)如果一个四边形一定能折成“叠加矩形”,那么它必须满足的条件是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】某小学开展4种课外兴趣小组活动,分别为A;绘画:B;机器人:C;跳舞:D;吉他.每个学生都要选取一个兴趣小组参与活动,小明对同学们选取的活动形式进行了随机抽样调查,根据调查统计结果,绘制了如下的统计图:
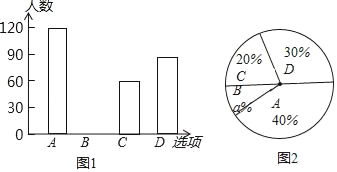
(1)本次调查学生共 人,a= ,并将条形图补充完整;
(2)如果该校有学生500人,则选择“机器人”活动的学生估计有多少人?
(3)学校让每班同学在A,B,C,D四种活动形式中,随机抽取两种开展活动,请用树状图或列表法的方法,求每班抽取的两种形式恰好是“绘画”和“机器人”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com