
科目: 来源: 题型:
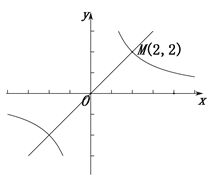
【题目】如图,在平面直角坐标系xOy中,一次函数![]() 与反比例函数
与反比例函数![]() (k≠0)的图象相交于点
(k≠0)的图象相交于点![]() .
.
(1)求k的值;
(2)点![]() 是y轴上一点,过点P且平行于x轴的直线分别与一次函数
是y轴上一点,过点P且平行于x轴的直线分别与一次函数![]() 、反比例函数
、反比例函数![]() 的图象相交于点
的图象相交于点![]() 、
、![]() ,当
,当![]() 时,画出示意图并直接写出a的取值范围.
时,画出示意图并直接写出a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某书店开展优惠售书活动,一次购书定价不超过200元的打九折;一次购书定价超过200元的,其中200元按九折计算,超过200元的部分打八折.小丽挑选了几本喜爱的书,计算定价后,准备支付144元,遇见同学小芳也在买书,计算小芳购书的定价后,小丽对小芳说:我们独自付款,都只能享受九折,合在一-起付款,按今天的活动一共可优惠 48元.请根据以上内容解答下列问题:
(1)小丽购书的定价是____元 .
(2)列方程求解小芳购书的定价.
查看答案和解析>>
科目: 来源: 题型:
【题目】近些年全国各地频发雾霾天气,给人民群众的身体健康带来了危害,某商场看到商机后决定购进甲、乙两种空气净化器进行销售.若每台甲种空气净化器的进价比每台乙种空气净化器的进价少300元,且用6000元购进甲种空气净化器的数量与用7500元购进乙种空气净化器的数量相同.
(1)求每台甲种空气净化器、每台乙种空气净化器的进价分别为多少元?
(2)若该商场准备进货甲、乙两种空气净化器共30台,且进货花费不超过42000元,问最少进货甲种空气净化器多少台?
查看答案和解析>>
科目: 来源: 题型:
【题目】以下是通过折叠正方形纸片得到等边三角形的步骤取一张正方形的纸片进行折叠,具体操作过程如下:
第一步:如图,先把正方形ABCD对折,折痕为MN;
第二步:点E在线段MD上,将△ECD沿EC翻折,点D恰好落在MN上,记为点P,连接BP可得△BCP是等边三角形
问题:在折叠过程中,可以得到PB=PC;依据是________________________.
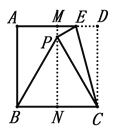
查看答案和解析>>
科目: 来源: 题型:
【题目】如图:已知![]() ,对应的坐标如下,请利用学过的变换(平移、旋转、轴对称)知识经过若干次图形变化,使得点A与点E重合、点B与点D重合,写出一种变化的过程_____.
,对应的坐标如下,请利用学过的变换(平移、旋转、轴对称)知识经过若干次图形变化,使得点A与点E重合、点B与点D重合,写出一种变化的过程_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】某中学举办运动会,在1500米的项目中,参赛选手在200米的环形跑道上进行,下图记录了跑得最快的一位选手与最慢的一位选手的跑步全过程(两人都跑完了全程),其中x代表的是最快的选手全程的跑步时间,y代表的是这两位选手之间的距离,下列说不合理的是()
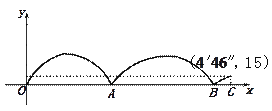
A. 出发后最快的选手与最慢的选手相遇了两次;
B. 出发后最快的选手与最慢的选手第一次相遇比第二次相遇的用时短;
C. 最快的选手到达终点时,最慢的选手还有415米未跑;
D. 跑的最慢的选手用时![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,如图,抛物线![]() 与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在![]() 轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
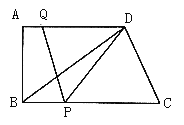
【题目】如图所示,在四边形ABCD中,AD//BC,∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒).
(1)设△DPQ的面积为S,求S与t之间的函数关系式;
(2)分别求出出当t为何值时,①PD=PQ,②DQ=PQ?
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料:
材料1、若一元二次方程ax2+bx+c=0(a≠0)的两根为x1,x2,则x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
材料2、已知实数m、n满足m2﹣m﹣1=0,n2﹣n﹣1=0,且m≠n,求![]() 的值.
的值.
解:由题知m、n是方程x2﹣x﹣1=0的两个不相等的实数根,根据材料1得
m+n=1,mn=﹣1
∴![]()
根据上述材料解决下面问题;
(1)一元二次方程2x2+3x﹣1=0的两根为x1、x2,则x1+x2= ,x1x2= .
(2)已知实数m、n满足2m2﹣2m﹣1=0,2n2﹣2n﹣1=0,且m≠n,求m2n+mn2的值.
(3)已知实数p、q满足p2=3p+2,2q2=3q+1,且p≠2q,求p2+4q2的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平行四边形OABC中,已知点A、C两点的坐标为A (![]() ,
,![]() ),C (2
),C (2![]() ,0).
,0).
(1)求点B的坐标.
(2)将平行四边形OABC向左平移![]() 个单位长度,求所得四边形A′B′C′O′四个顶点的坐标.
个单位长度,求所得四边形A′B′C′O′四个顶点的坐标.
(3)求平行四边形OABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com