
科目: 来源: 题型:
【题目】为推动全面健身,县政府在城南新城新建体育休闲公园,公园设有A、B、C、D四个出入口供广大市民进出.
(1)小明的爸爸去公园进行体育锻炼,从出入口A进入的概率是________;
(2)张老师和小明的爸爸一起约定去参加锻炼,请用画树状图或列表法求他们选择从不同出入口进体育场的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1,B2,B3…都在直线![]() 上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=1,则点B2019的坐标是_________________.
上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=1,则点B2019的坐标是_________________.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,要使它成为菱形,那么需要添加的条件可以是( )

A.AC=BD B.AB=AC C.∠ABC=90°D.AC⊥BD
查看答案和解析>>
科目: 来源: 题型:
【题目】已知多项式![]() 是关于
是关于![]() 的二次二项式.
的二次二项式.
(1)请填空:![]() ______;
______;![]() ______;
______;![]() ______;
______;
(2)如图,若![]() ,
,![]() 两点在线段
两点在线段![]() 上,且
上,且![]() ,
,![]() ,
,![]() 两点分别是线段
两点分别是线段![]() ,
,![]() 的中点,且
的中点,且![]() ,求线段
,求线段![]() 的长;
的长;
![]()
(3)如图,若![]() ,
,![]() ,
,![]() 分别是数轴上
分别是数轴上![]() ,
,![]() ,
,![]() 三点表示的数,
三点表示的数,![]() 点与
点与![]() 点到原点的距离相等,且位于原点两侧,现有两动点
点到原点的距离相等,且位于原点两侧,现有两动点![]() 和
和![]() 在数轴上同时开始运动,其中点
在数轴上同时开始运动,其中点![]() 先以2个单位每秒的速度从
先以2个单位每秒的速度从![]() 点运动到
点运动到![]() 点,再以5个单位每秒的速度运动到
点,再以5个单位每秒的速度运动到![]() 点,最后以8个单位每秒的速度返回到
点,最后以8个单位每秒的速度返回到![]() 点停止运动;而动点
点停止运动;而动点![]() 先以2个单位每秒的速度从
先以2个单位每秒的速度从![]() 点运动到
点运动到![]() 点,再以12个单位每秒的速度返回到
点,再以12个单位每秒的速度返回到![]() 点停止运动.在此运动过程中,
点停止运动.在此运动过程中,![]() ,
,![]() 两点到
两点到![]() 点的距离是否会相等?若相等,请直接写出此时点
点的距离是否会相等?若相等,请直接写出此时点![]() 在数轴上表示的数;若不相等,请说明理由.
在数轴上表示的数;若不相等,请说明理由.
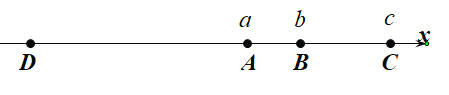
查看答案和解析>>
科目: 来源: 题型:
【题目】材料:思考的同学小斌在解决连比等式问题:“已知正数![]() ,
,![]() ,
,![]() 满足
满足![]() ,求
,求![]() 的值”时,采用了引入参数法
的值”时,采用了引入参数法![]() ,将连比等式转化为了三个等式,再利用等式的基本性质求出参数的值.进而得出
,将连比等式转化为了三个等式,再利用等式的基本性质求出参数的值.进而得出![]() ,
,![]() ,
,![]() 之间的关系,从而解决问题.过程如下:
之间的关系,从而解决问题.过程如下:
解;设![]() ,则有:
,则有:
![]() ,
,![]() ,
,![]() ,
,
将以上三个等式相加,得![]() .
.
![]()
![]() ,
,![]() ,
,![]() 都为正数,
都为正数,
![]()
![]() ,即
,即![]() ,.
,.
![]()
![]() .
.
仔细阅读上述材料,解决下面的问题:
(1)若正数![]() ,
,![]() ,
,![]() 满足
满足![]() ,求
,求![]() 的值;
的值;
(2)已知![]() ,
,![]() ,
,![]() ,
,![]() 互不相等,求证:
互不相等,求证:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料,回答问题:
材料一:
自然数的发现是人类数学研究的开端,我们在研究自然数的时候采用的进制为十进制.现定义:位数相同且对应数位上的数字之和为10的两个数互为“亲密数”,例如:3与7互为“亲密数”,16的“亲密数”为94.
材料二:
若![]() 的“亲密数”为
的“亲密数”为![]() ,记
,记![]() 为
为![]() 的“亲密差”例如:72的“亲密数”为38.
的“亲密差”例如:72的“亲密数”为38.
![]() ,则34为72的“亲密差”.
,则34为72的“亲密差”.
根据材料,回答下列问题:
(1)请填空:64的“亲密数”为______;25的“亲密差”为______;
(2)某两位数个位上的数字比十位上的数字大2,且这个两位数的“亲密数”等于它的![]() 倍,求这个两位数的“亲密差”:
倍,求这个两位数的“亲密差”:
(3)某个三位数![]() (
(![]() ,且
,且![]() 为整数),记
为整数),记 ,若
,若![]() 的值为一个整数,求这个整数
的值为一个整数,求这个整数![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
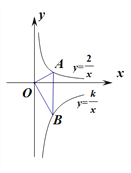
【题目】如图所示是一块含30°的直角三角板,直角顶点O位于坐标原点,斜边AB⊥x轴,顶点A在函数![]() (x>0)的图象上,顶点B在函数
(x>0)的图象上,顶点B在函数![]() (x>0)的图象上,∠ABO=30°,则k=_________.
(x>0)的图象上,∠ABO=30°,则k=_________.
查看答案和解析>>
科目: 来源: 题型:
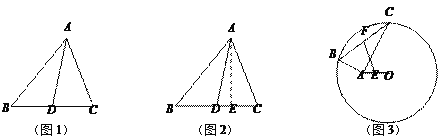
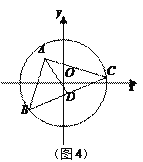
【题目】阅读理解:小明热爱数学,在课外书上看到了一个有趣的定理——“中线长定理”:三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍.如图1,在△ABC中,点D为BC的中点,根据“中线长定理”,可得:
AB2+AC2=2AD2+2BD2.
小明尝试对它进行证明,部分过程如下:
解:过点A作AE⊥BC于点E,如图2,在Rt△ABE中,AB2=AE2+BE2,
同理可得:AC2=AE2+CE2,AD2=AE2+DE2,
为证明的方便,不妨设BD=CD=x,DE=y,
∴AB2+AC2=AE2+BE2+AE2+CE2=……
(1)请你完成小明剩余的证明过程;
理解运用:
(2) ① 在△ABC中,点D为BC的中点,AB=6,AC=4,BC=8,则AD=_______;
② 如图3,⊙O的半径为6,点A在圆内,且OA=2![]() ,点B和点C在⊙O上,且∠BAC=90°,点E、F分别为AO、BC的中点,则EF的长为________;
,点B和点C在⊙O上,且∠BAC=90°,点E、F分别为AO、BC的中点,则EF的长为________;
拓展延伸:
(3)小明解决上述问题后,联想到《能力训练》上的题目:如图4,已知⊙O的半径为5![]() ,以A(3,4)为直角顶点的△ABC的另两个顶点B,C都在⊙O上,D为BC的中点,求AD长的最大值.请你利用上面的方法和结论,求出AD长的最大值.
,以A(3,4)为直角顶点的△ABC的另两个顶点B,C都在⊙O上,D为BC的中点,求AD长的最大值.请你利用上面的方法和结论,求出AD长的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,已知AB=AC=10cm,BC=16cm,AD⊥BC于D,点E、F分别从B、C两点同时出发,其中点E沿BC向终点C运动,速度为4cm/s;点F沿CA、AB向终点B运动,速度为5cm/s,设它们运动的时间为x(s).
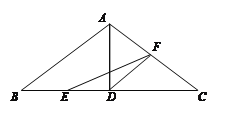
(1)求x为何值时,△EFC和△ACD相似;
(2)是否存在某一时刻,使得△EFD被 AD分得的两部分面积之比为3:5,若存在,求出x的值,若不存在,请说明理由;
(3)若以EF为直径的圆与线段AC只有一个公共点,求出相应x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com