
科目: 来源: 题型:
【题目】![]() 在平面直角坐标系的位置如图所示.
在平面直角坐标系的位置如图所示.
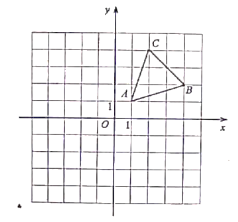
![]() 请作出
请作出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ,再作出
,再作出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ;
;
![]() 若点
若点![]() 为
为![]() 边
边![]() 上一点,则点
上一点,则点![]() 在
在![]() 上的对应点的坐标为_ ;
上的对应点的坐标为_ ;
![]() 点
点![]() 为
为![]() 轴上一点,且点
轴上一点,且点![]() 到点
到点![]() 的距高之和最短,请画出图形并写出点
的距高之和最短,请画出图形并写出点![]() 的坐标为_ .
的坐标为_ .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知二次函数![]() ,它与
,它与![]() 轴交于
轴交于![]() 、
、![]() ,且
,且![]() 、
、![]() 位于原点两侧,与
位于原点两侧,与![]() 的正半轴交于
的正半轴交于![]() ,顶点
,顶点![]() 在
在![]() 轴右侧的直线
轴右侧的直线![]() :
:![]() 上,则下列说法:①
上,则下列说法:①![]() ②
②![]() ③
③![]() ④
④![]() 其中正确的结论有( )
其中正确的结论有( )

A.①②B.②③C.①②③D.①②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知长方形ABCD中,AD=6cm,AB=4cm,点E为AD的中点.若点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BC上由点B向点C运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△AEP与△BPQ是否全等,请说明理由,并判断此时线段PE和线段PQ的位置关系;
(2)若点Q的运动速度与点P的运动速度相等,运动时间为t秒,设△PEQ的面积为Scm2,请用t的代数式表示S;
(3)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△AEP与△BPQ全等?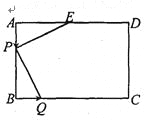
查看答案和解析>>
科目: 来源: 题型:
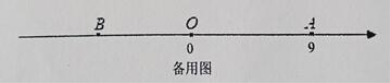
【题目】如图,已知数轴上点![]() 表示的数为9,
表示的数为9,![]() 是数轴上一点且
是数轴上一点且![]() .动点
.动点![]() 从点
从点![]() 出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为
出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为![]() (
(![]() )秒.
)秒.
![]()
发现:
(1)写出数轴上点![]() 表示的数 ,点
表示的数 ,点![]() 表示的数 (用含
表示的数 (用含![]() 的代数式表示);
的代数式表示);
探究:
(2)动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度沿数轴向左匀速运动, 若点
出发,以每秒2个单位长度的速度沿数轴向左匀速运动, 若点![]() 、
、![]() 同时出发,问
同时出发,问![]() 为何值时点
为何值时点![]() 追上点
追上点![]() ?此时
?此时![]() 点表示的数是多少?
点表示的数是多少?
(3)若![]() 是线段
是线段![]() 靠近点
靠近点![]() 的三等分点,
的三等分点,![]() 是线段
是线段![]() 靠近点
靠近点![]() 的三等分点.点
的三等分点.点![]() 在运动的过程中, 线段
在运动的过程中, 线段![]() 的长度是否发生变化?在备用图中画出图形,并说明理由.
的长度是否发生变化?在备用图中画出图形,并说明理由.

拓展:
(4)若点![]() 是数轴上点,点
是数轴上点,点![]() 表示的数是
表示的数是![]() ,请直接写:
,请直接写:![]() 的最小值是 .
的最小值是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
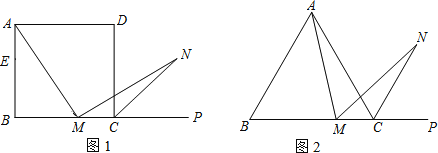
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连接ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】列方程解应用题:
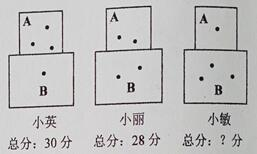
在课间活动中,小英、小丽和小敏在操场上画出![]() 、
、![]() 两个区域,一起玩投沙包游戏.沙包落在
两个区域,一起玩投沙包游戏.沙包落在![]() 区城所得分值与落在
区城所得分值与落在![]() 区域所得分值不同.当每人各投沙包四次时,其落点和四次总分如图所示.
区域所得分值不同.当每人各投沙包四次时,其落点和四次总分如图所示.
(1)求沙包每次落在![]() 、
、![]() 两个区域的分值各是多少?
两个区域的分值各是多少?
(2)请求出小敏的四次总分.

查看答案和解析>>
科目: 来源: 题型:
【题目】(1)问题背景
如图①,BC是⊙O的直径,点A在⊙O上,AB=AC,P为![]() 上一动点(不与B,C重合),
上一动点(不与B,C重合),
求证:![]() PA=PB+PC.
PA=PB+PC.

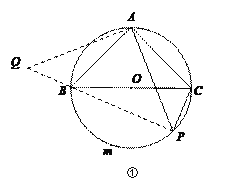
请你根据小明同学的思考过程完成证明过程.
(2)类比迁移
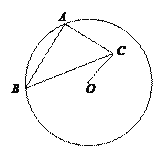
如图②,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=AC,AB⊥AC,垂足为A,求OC的最小值.

(3)拓展延伸
如图,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=![]() AC,AB⊥AC,垂足为A,则OC的最小值为 .
AC,AB⊥AC,垂足为A,则OC的最小值为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】直线![]() 上有一点
上有一点![]() ,过
,过![]() 作射线
作射线![]() ,嘉琪将一直角三角板的直角顶点与
,嘉琪将一直角三角板的直角顶点与![]() 重合.
重合.

(1)嘉琪把三角板![]() 如图1放置,若
如图1放置,若![]() ,则
,则![]() ,
,![]() ;
;
(2)嘉琪将直角三角板绕![]() 点顺时针旋转一定角度后如图2,使
点顺时针旋转一定角度后如图2,使![]() 平分
平分![]() ,且
,且![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】将若干枚棋子平均分成三堆(每堆至少2枚),分别放在左边、中间、右边,并按如下顺序进行操作:
第1次:从右边堆中拿出 2枚棋子放入中间一堆;
第2次:从左边一堆中拿出1枚棋子放入中间一堆;
第3次:从中间一堆中拿出几枚棋子放入右边一堆,并使右边一堆的棋子数为最初的2倍.
(1)操作结束后,若右边堆比左边一堆多15枚棋子,问共有_____枚棋子;
(2)通过计算得出:无论最初的棋子数为多少,按上述方法完成操作后,中间一堆总是剩下_____枚棋子.
查看答案和解析>>
科目: 来源: 题型:
【题目】某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间的关系可以近似地看作一次函数
(元)之间的关系可以近似地看作一次函数![]() .(利润=售价-制造成本)
.(利润=售价-制造成本)
(1)写出每月的利润![]() (万元)与销售单价
(万元)与销售单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月获得的利润为440万元?
(3)根据相关部门规定,这种电子产品的销售单价不能高于40元,如果厂商每月的制造成本不超过540万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com