
科目: 来源: 题型:
【题目】如图,直线y=kx(k<0)与双曲线![]() 交于A(x1,y1),B(x2,y2)两点,则3x1y2-5x2y1的值为 __________.
交于A(x1,y1),B(x2,y2)两点,则3x1y2-5x2y1的值为 __________.

【答案】-6
【解析】试题分析:∵点A(x1,y1),B(x2,y2)是双曲线y=![]() 上的点,
上的点,
∴x1y1=x2y2=-3①,
∵直线y=kx(k<0)与双曲线y=![]() 交于点A(x1,y1),B(x2,y2)两点,
交于点A(x1,y1),B(x2,y2)两点,
∴x1=-x2,y1=-y2②,
∴原式=-3x1y1+5x2y2=9-15=-6.
故答案为:-6.
点睛:本题考查的是反比例函数与一次函数的交点问题,反比例函数的对称性,根据反比例函数的图象关于原点对称得出x1=-x2,y1=-y2是解答此题的关键.
【题型】填空题
【结束】
15
【题目】A,B两地相距180km,新修的高速公路开通后,在A,B两地间行驶的长途客车平均车速提高了 50%,而从A地到B地的时间缩短了 1h .若设原来的平均车速为xkm/h,则根据题意可列方程为 _____________________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 落在线段
落在线段![]() 延长线上的点
延长线上的点![]() 处,点
处,点![]() 落在点
落在点![]() 处.
处.

(1)在图中画出旋转后得到的三角形;
(2)若旋转角的度数是![]() ,那么
,那么![]()
![]() .
.
(3)连接![]() ,
,
①若![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
②若![]() ,
,![]() ,则
,则![]() .(用含
.(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目: 来源: 题型:
【题目】某铁路桥长1000米.现有一列火车从桥上匀速通过.测得火车从开始上桥到完全通过桥共用了1分钟(即从车头进入桥头到车尾离开桥尾),整个火车完全在桥上的时间为40秒.
(1)如果设这列火车的长度为x米,填写下表(不需要化简):
火车行驶过程 | 时间(秒) | 路程(米) | 速度(米/秒) |
完全通过桥 | 60 | ||
整列车在桥上 | 40 |
(2)求这列火车的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线l有上三点M,O,N,MO=3,ON=1;点P为直线l上任意一点,如图画数轴.
![]()
(1)当以点O为数轴的原点时,点P表示的数为x,且点P到点M、点N的距离相等,那么x的值是________;
(2)当以点M为数轴的原点时,点P表示的数为y,当y= 时,使点P到点M、点N 的距离之和是5;
(3)若以点O为数轴的原点,点P以每秒2个单位长度的速度从点O向左运动时,点E从点M以每秒1个单位长度速度向左运动,点F从点N每秒3个单位长度的向左运动,且三点同时出发,求运动几秒时点P、点E、点F表示的数之和为-20.
查看答案和解析>>
科目: 来源: 题型:
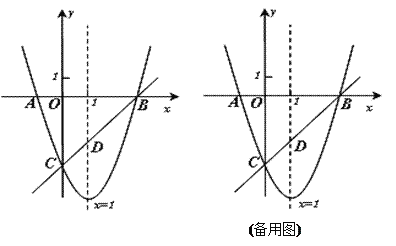
【题目】如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
⑴求抛物线的函数表达式;
⑵求直线BC的函数表达式;
⑶点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.①当线段PQ=![]() AB时,求tan∠CED的值;②当以点C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标.
AB时,求tan∠CED的值;②当以点C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知A,O,B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC,
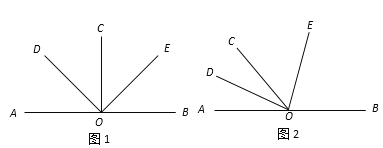
(1)若∠AOC=90°,如图1,则∠DOE= °;
(2)若∠AOC=50°,如图2,求∠DOE的度数;
(3)由上面的计算,你认为∠DOE= °;
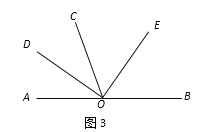
(4)若∠AOC=α,(0°< α <180°)如图3,求∠DOE的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】有一种公益叫“光盘”.所谓“光盘”,就是吃光你盘子中的食物,杜绝“舌尖上的浪费”.某校九年级开展“光盘行动”宣传活动,根据各班级参加该活动的总人次折线统计图,下列说法正确的是( )

A. 极差是40 B. 中位数是58 C. 平均数大于58 D. 众数是5
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,0是坐标原点,点A坐标为(2, 0),点B坐标为(0, b) (b>0), 点P是直线AB上位于第二象限内的一个动点,过点P作PC垂直于x轴于点C,记点P关于y轴的对称点为Q.
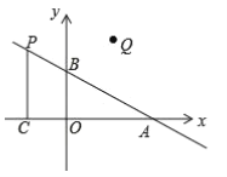
(1)当b=1时:①求直线AB相应的函数表达式:②若![]() ,求点P的坐标:
,求点P的坐标:
(2)设点P的横坐标为a,是否同时存在a、b,使得![]() 是等腰直角三角形?若存在,求出所有满足条件的a、b的值;若不存在,请说明理由.
是等腰直角三角形?若存在,求出所有满足条件的a、b的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,等腰直角三角形![]() 中,
中,![]() ,
,![]() .先将
.先将![]() 绕点
绕点![]() 逆时针方向旋转
逆时针方向旋转![]() ,得到
,得到![]() ,点
,点![]() 对应点
对应点![]() ,点
,点![]() 对应点
对应点![]() ;再将
;再将![]() 沿
沿![]() 方向平移,得到
方向平移,得到![]() ,点
,点![]() 、
、![]() 、
、![]() 的对应点分别是点
的对应点分别是点![]() 、
、![]() 、
、![]() ,设平移的距离为
,设平移的距离为![]() ,且
,且![]() .
.
(1)在图中画出![]() 和
和![]() ;
;
(2)记![]() 与
与![]() 的交点为点
的交点为点![]() ,
,![]() 与
与![]() 的交点为点
的交点为点![]() ,如果四边形
,如果四边形![]() 的面积是
的面积是![]() 的面积的3倍,试求四边形
的面积的3倍,试求四边形![]() 和
和![]() 的面积的比值.
的面积的比值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,AB∥CD,点P为定点,E、F分别是AB、CD上的动点.
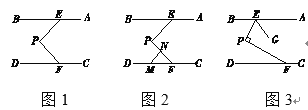
(1)求证:∠P=∠BEP+∠PFD;
(2)若点M为CD上一点,如图2,∠FMN=∠BEP,且MN交PF于N.试说明∠EPF与∠PNM的数量关系,并证明你的结论;
(3)移动E、F使得∠EPF=90°,如图3,作∠PEG=∠BEP,求∠AEG与∠PFD度数的比值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com