
科目: 来源: 题型:
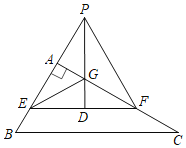
【题目】在Rt△ABC中,∠BAC=90°,E,F分别是AB,AC上的点,且EF∥BC,作EG平分∠AEF交AC于点G,在EF上取点D,使ED=EA,连接DG并延长,交BA的延长于点P,连接PF.
(1)求证:PD⊥EF;
(2)若ED=DF,求∠B的大小.
(3)在(2)的条件下,若四边形AEDG的面积为S,请直接写出△PEF的面积(用含S的式子表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=(x-a)(x-3)(0<a<3)的图象与x轴交于点A、B(点A在点B的左侧),与y轴交于点D,过其顶点C作直线CP⊥x轴,垂足为点P,连接AD、BC.
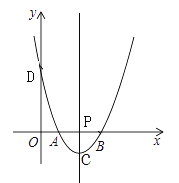
(1)求点A、B、D的坐标;
(2)若△AOD与△BPC相似,求a的值;
(3)点D、O、C、B能否在同一个圆上,若能,求出a的值,若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年2月14日,备受关注的《成都市中小学课后服务实施意见》正式出台.某区为了解“家长更希望如何安排孩子放学后的时间”,对该区七年级部分家长进行了一次问卷调查(每位同学只选择一位家长参与调查),将调查结果(![]() .回家,家人陪伴;
.回家,家人陪伴;![]() .学校课后延时服务;
.学校课后延时服务;![]() .校外培训机构;
.校外培训机构;![]() .社会托管班)绘制成以下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
.社会托管班)绘制成以下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
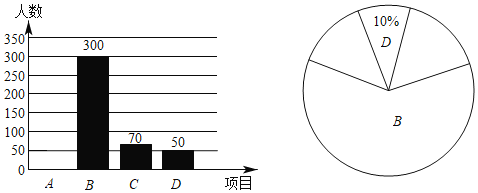
(1)本次调查的家长总人数为 ;
(2)补全条形统计图:扇形统计图中,![]() 类所对应的圆心角为 度;
类所对应的圆心角为 度;
(3)若该区共有七年级学生![]() 人,则愿意参加“学生课后延时服务”的人数大概是多少?
人,则愿意参加“学生课后延时服务”的人数大概是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】某书报亭开设两种租书方式:一种是零星租书,每册收费1元;另一种是会员卡租书,办卡费每月12元,租书费每册0.4元.小军经常来该店租书,若每月租书数量为x册.
(1)写出零星租书方式应付金额![]() (元)与租书数量x(册)之间的函数关系式。
(元)与租书数量x(册)之间的函数关系式。
(2)写出会员卡租书方式应付金额![]() (元)与租书数量x(册)之间的函数关系式.
(元)与租书数量x(册)之间的函数关系式.
(3)小军选取哪种租书方式更合算?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,D是BC的中点,点E在AD上.
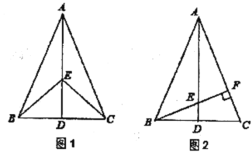
(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其他条件不变.求证:EF=CF.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:![]() ,OB,OM,ON是
,OB,OM,ON是![]() 内的射线.
内的射线.
![]() 如图1,若OM平分
如图1,若OM平分![]() ,ON平分
,ON平分![]() 当射线OB绕点O在
当射线OB绕点O在![]() 内旋转时,
内旋转时,![]() ______度
______度![]()
![]() 也是
也是![]() 内的射线,如图2,若
内的射线,如图2,若![]() ,OM平分
,OM平分![]() ,ON平分
,ON平分![]() ,当
,当![]() 绕点O在
绕点O在![]() 内旋转时,求
内旋转时,求![]() 的大小.
的大小.
![]() 在
在![]() 的条件下,若
的条件下,若![]() ,当
,当![]() 在
在![]() 绕O点以每秒
绕O点以每秒![]() 的速度逆时针旋转t秒,如图3,若
的速度逆时针旋转t秒,如图3,若![]() :
:![]() :3,求t的值.
:3,求t的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7,
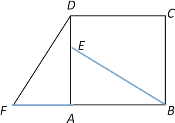
求:(1)指出旋转中心和旋转角度
(2)求DE的长度
(3)BE与DF的位置关系如何?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB,AC分别是半⊙O的直径和弦,OD⊥AC于点D,过点A作半⊙O的切线AP,AP与OD的延长线交于点P.连接PC并延长与AB的延长线交于点F.
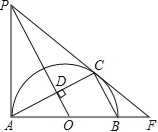
(1)求证:PC是半⊙O的切线;
(2)若∠CAB=30°,AB=10,求线段BF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,为了测量山坡上一棵树PQ的高度,小明在点A处利用测角仪测得树顶P的仰角为450 ,然后他沿着正对树PQ的方向前进10m到达B点处,此时测得树顶P和树底Q的仰角分别是600和300,设PQ垂直于AB,且垂足为C.
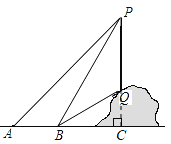
(1)求∠BPQ的度数;
(2)求树PQ的高度(结果精确到0.1m, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com