
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于任意三点A、B、C我们给出如下定义:“横长”a:三点中横坐标的最大值与最小值的差,“纵长”b:三点中纵坐标的最大值与最小值的差,若三点的横长与纵长相等,我们称这三点为正方点.
中,对于任意三点A、B、C我们给出如下定义:“横长”a:三点中横坐标的最大值与最小值的差,“纵长”b:三点中纵坐标的最大值与最小值的差,若三点的横长与纵长相等,我们称这三点为正方点.
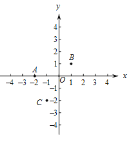
例如:点![]() (
(![]() ,0) ,点
,0) ,点 ![]() (1,1) ,点
(1,1) ,点 ![]() (
(![]() ,
, ![]() ),则
),则![]() 、
、![]() 、
、![]() 三点的 “横长”
三点的 “横长”![]() =|
=|![]() |=3,
|=3,![]() 、
、![]() 、
、![]() 三点的“纵长”
三点的“纵长”![]() =|
=|![]() |=3. 因为
|=3. 因为![]() =
=![]() ,所以
,所以![]() 、
、![]() 、
、![]() 三点为正方点.
三点为正方点.
(1)在点![]() (3,5) ,
(3,5) ,![]() (3,
(3,![]() ) ,
) ,![]() (
(![]() ,
,![]() )中,与点
)中,与点![]() 、
、![]() 为正方点的是 ;
为正方点的是 ;
(2)点P (0,t)为![]() 轴上一动点,若
轴上一动点,若![]() ,
,![]() ,
,![]() 三点为正方点,
三点为正方点,![]() 的值为 ;
的值为 ;
(3)已知点![]() (1,0).
(1,0).
①平面直角坐标系中的点![]() 满足以下条件:点
满足以下条件:点![]() ,
,![]() ,
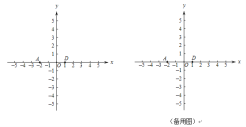
,![]() 三点为正方点,在图中画出所有符合条件的点
三点为正方点,在图中画出所有符合条件的点![]() 组成的图形;
组成的图形;
②若直线![]() :
:![]() 上存在点
上存在点![]() ,使得
,使得![]() ,
,![]() ,
,![]() 三点为正方点,直接写出m的取值范围.
三点为正方点,直接写出m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
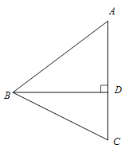
【题目】如图,在△ABC中,AB=AC>BC,BD 是AC边上的高,点C关于直线BD的对称点为点E,连接BE.
(1)①依题意补全图形;
②若∠BAC=![]() ,求∠DBE的大小(用含
,求∠DBE的大小(用含![]() 的式子表示);
的式子表示);
(2)若DE=2AE,点F是BE中点,连接AF,BD=4,求AF的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,结果为F(n)=3n+1;②当n为偶数时,结果为F(n)=![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行.例如,取n=13,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行.例如,取n=13,则:
![]()
若n=24,则第100次“F”运算的结果是_____
查看答案和解析>>
科目: 来源: 题型:
【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为( )
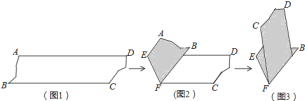
A.120°B.108°C.126°D.114°
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() ,与x轴交于A、B两点(点A在点B的左侧).
,与x轴交于A、B两点(点A在点B的左侧).
(1)求点A和点B的坐标;
(2)若点P(m,n)是抛物线上的一点,过点P作x轴的垂线,垂足为点D.
①在![]() 的条件下,当
的条件下,当![]() 时,n的取值范围是
时,n的取值范围是![]() ,求抛物线的表达式;
,求抛物线的表达式;
②若D点坐标(4,0),当![]() 时,求a的取值范围.
时,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知AB=AC,BE=CE,下面四个结论:①BP=CP;②AD⊥BC;③AE平分∠BAC;④∠PBC=∠PCB.其中正确的结论个数有( )个.
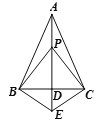
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,已知点A(0,a),点B(b,0),其中a,b满足![]() =0,点C(m,n)在第一象限,已知
=0,点C(m,n)在第一象限,已知![]() 是2的立方根.
是2的立方根.

(1)直接写出A,B,C三点的坐标;
(2)求出△ABC的面积;
(3)如图2,延长BC交y轴于D点,求点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com