
【题目】在平面直角坐标系![]() 中,对于任意三点A、B、C我们给出如下定义:“横长”a:三点中横坐标的最大值与最小值的差,“纵长”b:三点中纵坐标的最大值与最小值的差,若三点的横长与纵长相等,我们称这三点为正方点.
中,对于任意三点A、B、C我们给出如下定义:“横长”a:三点中横坐标的最大值与最小值的差,“纵长”b:三点中纵坐标的最大值与最小值的差,若三点的横长与纵长相等,我们称这三点为正方点.
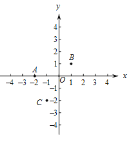
例如:点![]() (
(![]() ,0) ,点
,0) ,点 ![]() (1,1) ,点
(1,1) ,点 ![]() (
(![]() ,
, ![]() ),则
),则![]() 、
、![]() 、
、![]() 三点的 “横长”
三点的 “横长”![]() =|
=|![]() |=3,
|=3,![]() 、
、![]() 、
、![]() 三点的“纵长”
三点的“纵长”![]() =|
=|![]() |=3. 因为
|=3. 因为![]() =
=![]() ,所以
,所以![]() 、
、![]() 、
、![]() 三点为正方点.
三点为正方点.
(1)在点![]() (3,5) ,
(3,5) ,![]() (3,
(3,![]() ) ,
) ,![]() (
(![]() ,
,![]() )中,与点
)中,与点![]() 、
、![]() 为正方点的是 ;
为正方点的是 ;
(2)点P (0,t)为![]() 轴上一动点,若
轴上一动点,若![]() ,
,![]() ,
,![]() 三点为正方点,
三点为正方点,![]() 的值为 ;
的值为 ;
(3)已知点![]() (1,0).
(1,0).
①平面直角坐标系中的点![]() 满足以下条件:点
满足以下条件:点![]() ,
,![]() ,
,![]() 三点为正方点,在图中画出所有符合条件的点
三点为正方点,在图中画出所有符合条件的点![]() 组成的图形;
组成的图形;
②若直线![]() :
:![]() 上存在点
上存在点![]() ,使得
,使得![]() ,
,![]() ,
,![]() 三点为正方点,直接写出m的取值范围.
三点为正方点,直接写出m的取值范围.
【答案】(1)点 R;(2)2或3;(3)①见解析;② ![]() 或
或![]()
【解析】(1)根据正方点的定义即可判断;(2)根据正方点的定义构建方程即可解决问题;(3) ①根据正方点的定义画出图形即可; ②如图,当直线y=![]() 与①中的图象有交点时满足条件,求出直线经过M(1,3)或(-2,-3)时b的值即可解决问题.
与①中的图象有交点时满足条件,求出直线经过M(1,3)或(-2,-3)时b的值即可解决问题.
(1)根据正方点的定义,可知点![]() 与A、B是正方点.
与A、B是正方点.
(2)由题意:t-0=1-(-2)或1-t=1-(-2),故答案为:2或3;
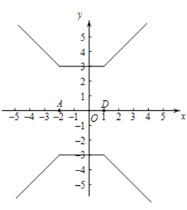
(3)①画出如图所示的图像
②如图,当直线y=![]() 与①中的图象有交点时满足条件.
与①中的图象有交点时满足条件.
当直线y=![]() 经过图中M(1,3)时,3=
经过图中M(1,3)时,3=![]() +b,解得b=
+b,解得b=![]() ,
,
当直线y=![]() 经过图中N(-2,-3)时,-3=-1+b,解得b=-2.
经过图中N(-2,-3)时,-3=-1+b,解得b=-2.
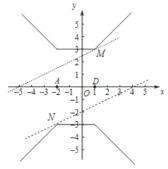
观察图象可知:m≥![]() 或m<-2时,y=
或m<-2时,y=![]() 上存在点N,使得A、D、N三点为正方点.
上存在点N,使得A、D、N三点为正方点.


科目:初中数学 来源: 题型:
【题目】某旅游公司大巴从旅行社出发,先向西行驶3千米到达![]() 景点,再继续向西行驶2千米到达
景点,再继续向西行驶2千米到达![]() 景点,然后向东行驶7千米到达
景点,然后向东行驶7千米到达![]() 景点,最后回到旅行社.
景点,最后回到旅行社.
(1)以旅行社为原点,以向东方向为正方向,用1个单位长度表示1千米,画出数轴,并在该数轴上表示出![]() 、
、![]() 、
、![]() 三个景点的位置.
三个景点的位置.
(2)![]() 景点距离
景点距离![]() 景点多远?
景点多远?
(3)该旅游大巴共行驶了多少路程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离y(千米)与行驶时间x(小时)的对应关系如图所示,下列叙述正确的是( )

A. 甲乙两地相距1200千米
B. 快车的速度是80千米∕小时
C. 慢车的速度是60千米∕小时
D. 快车到达甲地时,慢车距离乙地100千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上线段AB=2(单位长度),CD=4(单位长度),点A在数轴上表示的数是﹣8,点C在数轴上表示的数是10,若线段 AB以6个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的数度也向右匀速运动.
![]()
(1)运动t秒后,点B表示的数是 ;点C表示的数是 ;(用含有t的代数式表示)
(2)求运动多少秒后,BC=4(单位长度);
(3)P是线段AB上一点,当B点运动到线段CD上,且点P不在线段CD上时,是否存在关系式 BD﹣AP=3PC.若存在,求线段PD的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
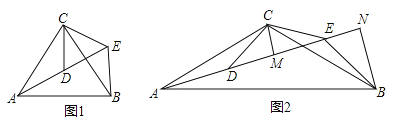
【题目】(2016山东省菏泽市)如图,△ACB和△DCE均为等腰三角形,点A,D,E在同一直线上,连接BE.
(1)如图1,若∠CAB=∠CBA=∠CDE=∠CED=50°
①求证:AD=BE;
②求∠AEB的度数.
(2)如图2,若∠ACB=∠DCE=120°,CM为△DCE中DE边上的高,BN为△ABE中AE边上的高,试证明:AE=![]() CM+
CM+![]() BN.
BN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中有 A(-2,1), B(3, 1),C(2, 3)三点,请回答下列问题:

(1)在坐标系内描出点A, B, C的位置.
(2)画出![]() 关于直线x=-1对称的
关于直线x=-1对称的![]() ,并写出
,并写出![]() 各点坐标.
各点坐标.
(3)在y轴上是否存在点P,使以A,B, P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A1(1,0),A2(1,﹣1),A3(﹣1,﹣1),A4(﹣1,1),A5(2,1),…则点A2017的坐标是( )
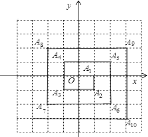
A.(505,504)B.(﹣503,﹣504 )C.(503,﹣503)D.(﹣504,504)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com