
科目: 来源: 题型:
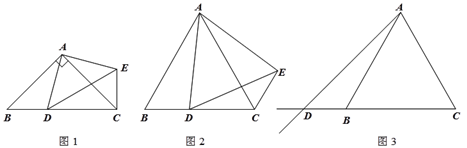
【题目】在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE= 度;
(2)设∠BAC= ![]() ,∠DCE=
,∠DCE= ![]() .
.
① 如图2,当点D在线段CB上,∠BAC≠90°时,请你探究![]() 与
与![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
② 如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,并直接写出此时![]() 与
与![]() 之间的数量关系(不需证明).
之间的数量关系(不需证明).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图, AD 为△ ABC 的中线, BE 为△ ABD 的中线.

(1)∠ ABE=15°,∠ BED=55°,求∠ BAD 的度数;
(2)作△ BED 的边 BD 边上的高;
(3)若△ ABC 的面积为 20, BD=2.5,求△ BDE 中 BD 边上的高.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在射线OM上有三点A,B,C,满足OA=20cm,AB=60cm,BC=10cm,点P从点O出发,沿OM方向以1cm/s的速度运动,点Q从点C出发在线段CO上向点O匀速运动(点Q运动到点O时停止运动),两点同时出发.
(1)当PA=2PB(P在线段AB上)时,点Q运动到的位置恰好是线段AB的中点,求点Q的运动速度;
(2)若点Q的运动速度为3cm/s,经过多长时间P,Q两点相距70cm?
(3)当点P运动到线段AB上时,分别取OP和AB的中点E,F,求![]() .
.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知∠AOB=90°,射线OC绕点O从OA位置开始,以每秒4°的速度顺时针方向旋转;同时,射线OD绕点O从OB位置开始,以每秒1°的速度逆时针方向旋转.当OC与OA成180°时,OC与OD同时停止旋转.

(1)当OC旋转10秒时,∠COD= °.
(2)当旋转时间为 秒时,OC与OD的夹角是30°.
(3)当旋转时间为 秒时,OB平分∠COD时.
查看答案和解析>>
科目: 来源: 题型:
【题目】某水果零售商店分两批次从批发市场共购进“红富士”苹果100箱,已知第一、二次进货价分别为每箱50元、40元,且第二次比第一次多付款400元.
(1)求第一、二次分别购进“红富士”苹果各多少箱?
(2)商店对这100箱“红富士”苹果先按每箱60元销售了75箱后出现滞销,于是决定其余的每箱靠打折销售完.要使商店销售完全部“红富士”苹果所获得的利润不低于1300元,问其余的每箱至少应打几折销售?(注:按整箱出售,利润=销售总收人﹣进货总成本)
查看答案和解析>>
科目: 来源: 题型:
【题目】把 6个相同的小正方体摆成如图的几何体.
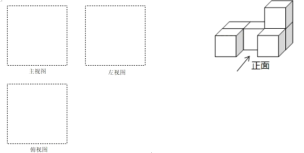
(1)画出该几何体的主视图、左视图、俯视图;
(2)如果每个小正方体棱长为![]() ,则该几何体的表面积是
,则该几何体的表面积是 ![]() .
.
(3)如果在这个几何体上再添加一些相同的小正方体,并并保持左视图和俯视图不变,那么最多可以再 添加 个小正方体.
查看答案和解析>>
科目: 来源: 题型:
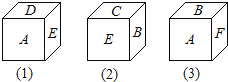
【题目】一个小立方体的六个面分别标有字母A、B、C、D、E、F,从三个不同方向看到的情形如图.
(1)A对面的字母是_____,B对面的字母是_____,E对面的字母是_____.(请直接填写答案)
(2)若A=2x﹣1,B=﹣3x+9,C=﹣5,D=1,E=4x+5,F=9,且字母A与它对面的字母表示的数互为相反数,求B、E的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com