科目： 来源： 题型：
【题目】如图，四边形ABCD是边长为1的正方形，E，F为BD所在直线上的两点．若AE= 
，∠EAF=135°，则以下结论正确的是（ ）
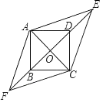
A. DE=1 B. tan∠AFO= 
C. AF= 
D. 四边形AFCE的面积为 
查看答案和解析>>
科目： 来源： 题型：
【题目】阅读材料：如果一个数的平方等于
，记为记
，这个数
叫做虚数单位，那么形如
(
为实数)的数就叫做复数，
叫这个复数的实部，
叫做这个复数的虚部。它有如下特点：①它的加，减，乘法运算与整式的加，减，乘法运算类似。例如计算：
；
②若他们的实部和虚部分别相等，则称这两个复数相等；若它们的实部相等，虚部互为相反数，则称这两个复数共轭，如
的共轭复数为
。
（1）填空：
；
。
（2）求
的共轭复数：
（3）已知
，其中
为正整数，求
的值；
查看答案和解析>>
科目： 来源： 题型：
【题目】我们知道，同底数幂的乘法法则为：am·an＝am＋n(其中a≠0，m，n为正整数)，类似地我们规定关于任意正整数m，n的一种新运算：h(m＋n)＝h(m)·h(n)，请根据这种新运算填空：
(1)若h(1)＝
，则h(2)＝________；
(2)若h(1)＝k(k≠0)，则h(n)·h(2017)＝________(用含n和k的代数式表示，其中n为正整数)．
查看答案和解析>>
科目： 来源： 题型：
【题目】如果一个正整数可以表示为两个连续奇数的平方差，那么称该正整数为“和谐数”如（8=32﹣12，16=52﹣32，即8，16均为“和谐数”），在不超过2017的正整数中，所有的“和谐数”之和为（ ）
A. 255054 B. 255064 C. 250554 D. 255024
查看答案和解析>>
科目： 来源： 题型：
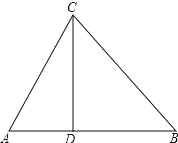
【题目】某校要在一块三角形空地上种植花草，如图所示，AC＝13 米、AB＝14 米、BC＝15 米， 若线段 CD 是一条引水渠，且点 D 在边 AB 上．已知水渠的造价每米 150 元．问：点 D 与点 C 距离多远时，水渠的造价最低？最低造价是多少元？
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，在边长为2m+3的正方形纸片中剪出一个边长为m+3的正方形之后，剩余部分可剪拼成一个长方形，
（1）求拼接成的长方形面积．
（2）若拼成的长方形一边长为 m，求此长方形的周长．
查看答案和解析>>
科目： 来源： 题型：
【题目】近年来市政府每年出资新建一批廉租房，使城镇住房困难的居民住房状况得到改善.下面是某小区2006～2008年每年人口总数和人均住房面积的统计的折线图(人均住房面积=该小区住房总面积/该小区人口总数，单位：㎡/人).
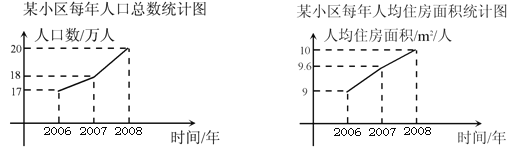
根据以上信息，则下列说法：①该小区2006～2008年这三年中，2008年住房总面积最大；②该小区2007年住房总面积达到1.728×106 m
；③该小区2008年人均住房面积的增长率为4%.其中正确的有
（A）①②③（B）①②（C）① （D）③
查看答案和解析>>
科目： 来源： 题型：
【题目】在直角坐标系中，过原点O及点A（8，0），C（0，6）作矩形OABC、连结OB，点D为OB的中点，点E是线段AB上的动点，连结DE，作DF⊥DE，交OA于点F，连结EF．已知点E从A点出发，以每秒1个单位长度的速度在线段AB上移动，设移动时间为t秒．
（1）如图1，当t=3时，求DF的长．
（2）如图2，当点E在线段AB上移动的过程中，∠DEF的大小是否发生变化？如果变化，请说明理由；如果不变，请求出tan∠DEF的值．
（3）连结AD，当AD将△DEF分成的两部分的面积之比为1：2时，求相应的t的值．
查看答案和解析>>
科目： 来源： 题型：
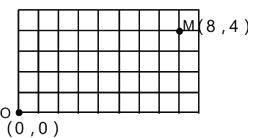
【题目】四个点的坐标分别是： A(0, 3) 、 B(2, 4) 、 C(6, 2) 、 D(5, 0) .
（1）在下面的方格中分别作出 A 、 B 、 C 、 D 四个点的位置；
（2）顺次连结 A 、 B 、 C 、 D 四个点，得到四边形 ABCD ,求四边形 ABCD 的面积．
查看答案和解析>>
科目： 来源： 题型：
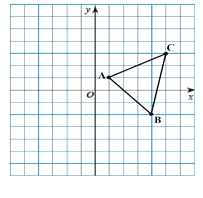
【题目】如图，在平面直角坐标系中， ABC 三个顶点的坐标分别为 A(1,1) ， B(4, 2) ，C (5, 3) .
（1）在图中画出 ABC 关于 y 轴的对称 图形 A1B1C1 ；（要求：画出三角形，标出相应顶点的 字母，不写结论）
（2）分别写出A1B1C1 三个顶点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com