
科目: 来源: 题型:
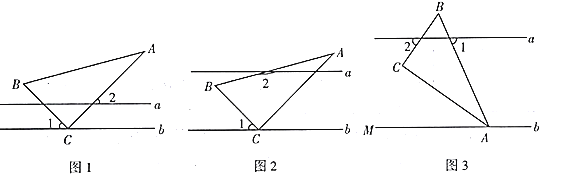
【题目】在综合与实践课上,同学们以“一个含![]() 的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线
的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线![]() 且
且![]() 和直角三角形
和直角三角形![]() ,
,![]() ,
,![]() ,
,![]() .
.
操作发现:
(1)在如图1中,![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,创新小组的同学把直线![]() 向上平移,并把
向上平移,并把![]() 的位置改变,发现
的位置改变,发现![]() ,说明理由;
,说明理由;
实践探究:
(3)缜密小组在创新小组发现结论的基础上,将如图中的图形继续变化得到如图,![]() 平分
平分![]() ,此时发现
,此时发现![]() 与
与![]() 又存在新的数量关系,请直接写出
又存在新的数量关系,请直接写出![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】某社区积极响应正在开展的“创文活动”,组织甲、乙两个志愿工程队对社区的一些区域进行绿化改造.已知甲工程队每小时能完成的绿化面积是乙工程队每小时能完成的绿化面积的2倍,并且甲工程队完成300平方米的绿化面积比乙工程队完成300平方米的绿化面积少用3小时,乙工程队每小时能完成多少平方米的绿化面积?
查看答案和解析>>
科目: 来源: 题型:
【题目】2017年12月8日,以“[数字工匠]玉汝于成,[数字工坊]溪达四海”为主题的2017一带一路数学科技文化节玉溪暨第10届全国三维数字化创新设计大赛(简称“全国3D大赛”)总决赛在玉溪圆满闭幕.某学校为了解学生对这次大赛的了解程度,在全校1300名学生中随机抽取部分学生进行了一次问卷调查,并根据收集到的信息进行了统计,绘制了下面两幅统计图.下列四个选项错误的是( )
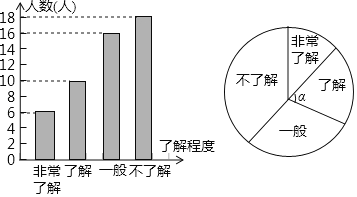
A. 抽取的学生人数为50人
B. “非常了解”的人数占抽取的学生人数的12%
C. a=72°
D. 全校“不了解”的人数估计有428人
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() 的三个顶点坐标分别是
的三个顶点坐标分别是![]() ,
,![]() ,
,![]() .
.
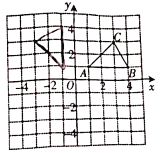
(1)将入![]() 向下平移
向下平移![]() 个单位后得到
个单位后得到![]() ,请画出
,请画出![]() ;
;
(2)将![]() 绕原点
绕原点![]() 逆时针旋转
逆时针旋转![]() 后得到
后得到![]() ,请画出
,请画出![]() ;
;
(3)判断以![]() 、
、![]() 、
、![]() 为顶点的三角形的形状.(无须说明理由)
为顶点的三角形的形状.(无须说明理由)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+bx(a≠0)的图象过原点O和点A(1, ![]() ),且与x轴交于点B,△AOB的面积为
),且与x轴交于点B,△AOB的面积为![]() 。
。
(1)求抛物线的解析式;
(2)若抛物线的对称轴上存在一点M,使△AOM的周长最小,求M点的坐标;
(3)点F是x轴上一动点,过F作x轴的垂线,交直线AB于点E,交抛物线于点P,且PE=![]() ,直接写出点E的坐标(写出符合条件的两个点即可)。
,直接写出点E的坐标(写出符合条件的两个点即可)。


查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图1,在矩形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,过点
,过点![]() 作直线
作直线![]() ,且交
,且交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,且
,且![]() 平分
平分![]() .
.
①求证:四边形![]() 是菱形;
是菱形;
②直接写出![]() 的度数;
的度数;

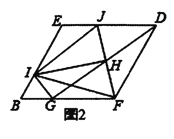
(2)把(1)中菱形![]() 进行分离研究,如图2,
进行分离研究,如图2,![]() 分别在
分别在![]() 边上,且
边上,且![]() ,连接
,连接![]() 为
为![]() 的中点,连接
的中点,连接![]() ,并延长
,并延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .试探究线段
.试探究线段![]() 与
与![]() 之间满足的关系,并说明理由;
之间满足的关系,并说明理由;
(3)把(1)中矩形![]() 进行特殊化探究,如图3,矩形
进行特殊化探究,如图3,矩形![]() 满足
满足![]() 时,点
时,点![]() 是对角线
是对角线![]() 上一点,连接
上一点,连接![]() ,作
,作![]() ,垂足为点
,垂足为点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() .请直接写出线段
.请直接写出线段![]() 三者之间满足的数量关系.
三者之间满足的数量关系.

查看答案和解析>>
科目: 来源: 题型:
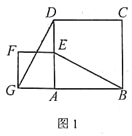
【题目】如图1,正方形ABCD和正方形AEFG,连接DG,BE。
(1)发现
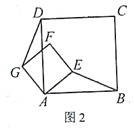
当正方形AEFG绕点A旋转,如图2,①线段DG与BE之间的数量关系是____________。②直线DG与直线BE之间的位置关系是____________。
(2)探究
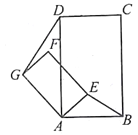
如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,证明:直线DG⊥BE
(3)应用
在(2)情况下,连结GE(点E在AB上方),若GE∥AB,且AB=![]() ,AE=1,则线段DG是多少?(直接写出结论)
,AE=1,则线段DG是多少?(直接写出结论)
查看答案和解析>>
科目: 来源: 题型:
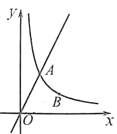
【题目】如图,直线y=2x与反比例函数![]() (k≠0,x>0)的图象交于点A(1,m),点B(n,t)是反比例函数图象上一点,且n=2t。
(k≠0,x>0)的图象交于点A(1,m),点B(n,t)是反比例函数图象上一点,且n=2t。
(1)求k的值和点B坐标;
(2)若点P在x轴上,使得△PAB的面积为2,直接写出点P坐标。
查看答案和解析>>
科目: 来源: 题型:
【题目】周末,小明乘坐家门口的公交车到和平公园游玩,他先乘坐公交车![]() 小时后达到书城,逗留一段时间后继续坐公交车到和平公园,小明出发一段时间后,小明的妈妈不放心,于是驾车沿相同的路线前往和平公园.如图是他们离家的路程
小时后达到书城,逗留一段时间后继续坐公交车到和平公园,小明出发一段时间后,小明的妈妈不放心,于是驾车沿相同的路线前往和平公园.如图是他们离家的路程![]() 与离家时间
与离家时间![]() 的关系图,请根据图回答下列问题:
的关系图,请根据图回答下列问题:
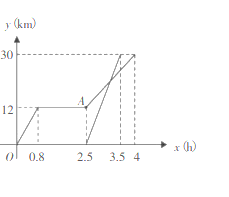
(1)小明家到和平公园的路程为 ![]() ,他在书城逗留的时间为 _
,他在书城逗留的时间为 _![]() ;
;
(2)图中![]() 点表示的意义是 ;
点表示的意义是 ;
(3)求小明从书城到和平公园的平均速度和小明的妈妈驾车的平均速度(平均速度![]() )
)
查看答案和解析>>
科目: 来源: 题型:
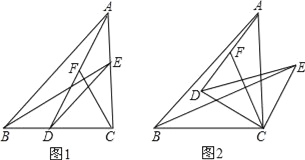
【题目】已知△ABC和△DEC都是等腰直角三角形,C为它们的公共直角顶点,D、E分别在BC、AC边上.
(1)如图1,F是线段AD上的一点,连接CF,若AF=CF;
①求证:点F是AD的中点;
②判断BE与CF的数量关系和位置关系,并说明理由;
(2)如图2,把△DEC绕点C顺时针旋转α角(0<α<90°),点F是AD的中点,其他条件不变,判断BE与CF的关系是否不变?若不变,请说明理由;若要变,请求出相应的正确结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com