
【题目】周末,小明乘坐家门口的公交车到和平公园游玩,他先乘坐公交车![]() 小时后达到书城,逗留一段时间后继续坐公交车到和平公园,小明出发一段时间后,小明的妈妈不放心,于是驾车沿相同的路线前往和平公园.如图是他们离家的路程
小时后达到书城,逗留一段时间后继续坐公交车到和平公园,小明出发一段时间后,小明的妈妈不放心,于是驾车沿相同的路线前往和平公园.如图是他们离家的路程![]() 与离家时间
与离家时间![]() 的关系图,请根据图回答下列问题:
的关系图,请根据图回答下列问题:
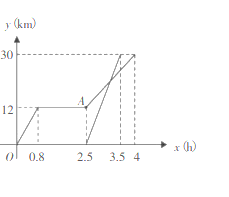
(1)小明家到和平公园的路程为 ![]() ,他在书城逗留的时间为 _
,他在书城逗留的时间为 _![]() ;
;
(2)图中![]() 点表示的意义是 ;
点表示的意义是 ;
(3)求小明从书城到和平公园的平均速度和小明的妈妈驾车的平均速度(平均速度![]() )
)
【答案】(1)30,1.7;(2)小明离家![]() 小时后离开书城,继续坐公交车到和平公园;(3)小明从书城到和平公园的平均速度是
小时后离开书城,继续坐公交车到和平公园;(3)小明从书城到和平公园的平均速度是![]() ,小明的妈妈驾车的平均速度
,小明的妈妈驾车的平均速度![]()
【解析】
(1)利用函数图像可得小明距离公园的路程为30千米,小明逗留的时间为:2.5-0.8时,从而求解;
(2)根据题意,利用函数图象可得点A表示小明离家![]() 小时后离开书城,继续坐公交车到和平公园;
小时后离开书城,继续坐公交车到和平公园;
(3)用平均速度=路程÷时间,即可求解.
解:(1)从图象可以看出,小明距离公园的路程为30千米,小明逗留的时间为:2.5-0.8=1.7,
故答案为30,1.7;
(2)图中![]() 点表示小明离家
点表示小明离家![]() 小时后离开书城,继续坐公交车到和平公园;
小时后离开书城,继续坐公交车到和平公园;
故答案为:小明离家![]() 小时后离开书城,继续坐公交车到和平公园;
小时后离开书城,继续坐公交车到和平公园;
(3)![]() ,
,
![]() .
.
答:小明从书城到和平公园的平均速度是![]() ,小明的妈妈驾车的平均速度
,小明的妈妈驾车的平均速度![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,数轴上的点A、B、C、D、E表示连续的五个整数,对应的数分别为a、b、c、d、e。
(1)若a+e=0,直接写出代数式b+c+d的值为_____;
(2)若a+b=7,先化简,再求值:![]() ;
;
(3)若a+b+c+d+e=5,数轴上的点M表示的实数为m,且满足MA+ME>12,则m的范围是____。
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
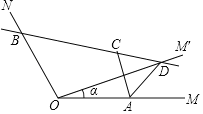
【题目】如图,已知∠MON=120°,点A,B分别在OM,ON上,且OA=OB=a,将射线OM绕点O逆时针旋转得到OM′,旋转角为α(0°<α<120°且α≠60°),作点A关于直线OM′的对称点C,画直线BC交OM′于点D,连接AC,AD,有下列结论:
①AD=CD;
②∠ACD的大小随着α的变化而变化;
③当α=30°时,四边形OADC为菱形;
④△ACD面积的最大值为![]() a2;
a2;
其中正确的是_____.(把你认为正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)
点A、B、C为数轴上三点,如果点C在A、B之间且到A的距离是点C到B的距离3倍,那么我们就称点C是{A,B}的奇点.
例如,如图1,点A表示的数为﹣3,点B表示的数为1.表示0的点C到点A的距离是3,到点B的距离是1,那么点C是{A,B}的奇点;又如,表示﹣2的点D到点A的距离是1,到点B的距离是3,那么点D就不是{A,B}的奇点,但点D是{B,A}的奇点.
(知识运用)
如图2,M、N为数轴上两点,点M所表示的数为﹣3,点N所表示的数为5.
(1)数 所表示的点是{M,N}的奇点;数 所表示的点是{N,M}的奇点;
(2)如图3,A、B为数轴上两点,点A所表示的数为﹣50,点B所表示的数为30.现有一动点P从点B出发向左运动,当P点运动到数轴上的什么位置时,P、A和B中恰有一个点为其余两点的奇点?

查看答案和解析>>
科目:初中数学 来源: 题型:
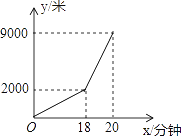
【题目】小亮早晨从家骑车到学校,先上坡后下坡,所行路程y(米)与时间x(分钟)的关系如图所示,若返回时上坡、下坡的速度仍与去时上、下坡的速度分别相同,则小明从学校骑车回家用的时间是________分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() 的三个顶点坐标分别是
的三个顶点坐标分别是![]() ,
,![]() ,
,![]() .
.
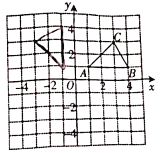
(1)将入![]() 向下平移
向下平移![]() 个单位后得到
个单位后得到![]() ,请画出
,请画出![]() ;
;
(2)将![]() 绕原点
绕原点![]() 逆时针旋转
逆时针旋转![]() 后得到
后得到![]() ,请画出
,请画出![]() ;
;
(3)判断以![]() 、
、![]() 、
、![]() 为顶点的三角形的形状.(无须说明理由)
为顶点的三角形的形状.(无须说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年10月17日7时30分,我国神舟十一号载人飞船在酒泉卫星发射中心发射升空,10月19日凌晨,神舟十一号飞船与天宫二号自动交会对接成功,32天后成功返回地面.这是中国人民的骄傲和自豪,受此鼓舞,某中学兴趣小组的同学们制作并发射了一枚小火箭,火箭发射台离地面的高度为2米,火箭离地面的高度![]() (米)与时间
(米)与时间![]() (秒)的关系如下表:
(秒)的关系如下表:
时间 | 高度 |
1 | 2+2 |
2 | 2+4 |
3 | 2+6 |
4 | 2+8 |
… | … |
(1)火箭发射10秒末离地面的高度为__________米;
(2)请你根据表中的数据写出火箭离地面的高度![]() 与时间
与时间![]() 的关系式:__________(用含
的关系式:__________(用含![]() 的式子表示
的式子表示![]() )
)
(3)利用公式求出当![]() 秒时,火箭离地面的高度.
秒时,火箭离地面的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
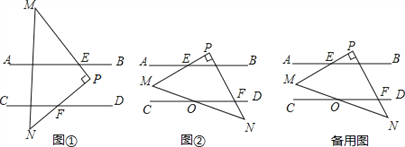
【题目】如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F
(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为 ;
(2)当△PMN所放位置如图②所示时,求证:∠PFD﹣∠AEM=90°;
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEB中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是

A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com