
科目: 来源: 题型:
【题目】(1)问题发现
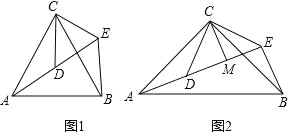
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.填空:
①∠AEB的度数为______;
②线段AD,BE之间的数量关系为______.
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣5与坐标轴交于A(﹣1,0),B(5,0),C(0,﹣5)三点,顶点为D.
(1)请直接写出抛物线的解析式及顶点D的坐标;
(2)连接BC与抛物线的对称轴交于点E,点P为线段BC上的一个动点(点P不与B、C两点重合),过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.
①是否存在点P,使四边形PEDF为平行四边形?若存在,求出点P的坐标;若不存在,说明理由.
②过点F作FH⊥BC于点H,求△PFH周长的最大值.

查看答案和解析>>
科目: 来源: 题型:
【题目】我们定义:
在一个三角形中,如果一个角的度数是另一个角的度数![]() 倍,那么这样的三角形我们称之为“和谐三角形”.如:三个内角分别为
倍,那么这样的三角形我们称之为“和谐三角形”.如:三个内角分别为![]() ,
,![]() ,
,![]() 的三角形是“和谐三角形”
的三角形是“和谐三角形”
概念理解:
如图,![]() ,在射线
,在射线![]() 上找一点
上找一点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为端点作射线
为端点作射线![]() ,交线段
,交线段![]() 于点
于点![]() (点
(点![]() 不与
不与![]() 重合)
重合)

(1)![]() 的度数为 ,
的度数为 ,![]() (填“是”或“不是”)“和谐三角形”
(填“是”或“不是”)“和谐三角形”
(2)若![]() ,求证:
,求证:![]() 是“和谐三角形”.
是“和谐三角形”.
应用拓展:
如图,点![]() 在
在![]() 的边
的边![]() 上,连接
上,连接![]() ,作
,作![]() 的平分线
的平分线![]() 交于点
交于点![]() ,在
,在![]() 上取点
上取点![]() ,使
,使![]() ,
,![]() .若
.若![]() 是“和谐三角形”,求
是“和谐三角形”,求![]() 的度数.
的度数.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知数轴上的A、B两点所对应的数分别为a、b.P为数轴上的一个动点.其中a,b满足(a﹣1)2+|b+5|=0,
(1)若点P为AB的中点,求P点对应的数.
(2)若点P从A点出发,以每秒2个单位的速度向左运动,t秒后,求P点所对应的数以及PB的距离.
(3)若数轴上点M、N所对应的数为m、n,其中A为PM的中点,B为PN的中点,无论点P在何处,![]() 是否为一个定值?若是,求出定值:若不是,请说明理由.
是否为一个定值?若是,求出定值:若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△ABD∽△DCP;
(3)当AB=5cm,AC=12cm时,求线段PC的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=120,AD⊥BC,且AD=AB.
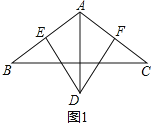
(1)如图1,DE⊥AB,DF⊥AC,垂足分别为点E,F,求证:AE+AF=AD
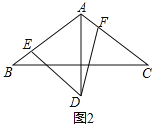
(2)如图2,如果∠EDF=60,且∠EDF两边分别交边AB,AC于点E,F,那么线段AE,AF,AD之间有怎样的数量关系?并给出证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了保障人畜饮水安全,某县急需饮水设备12台,现有甲、乙两种设备可供选择,已知购买1台甲种设备和2台乙两种设备共需10000元,购买3台甲种设备和1台乙两种设备共需15000元,且甲种设备的安装及运输费用为600元/台,乙种设备的安装及运输费用为800元/台.
(1)购买1台甲、乙两种设备各需多少元?
(2)若购买的费用不超过40000元,安装及运输费用不超过9200元,则有几种购买方案?
查看答案和解析>>
科目: 来源: 题型:
【题目】我国古代对于利用方程解决实际问题早有研究,《九章算术》中提到这么一道“以绳测井”的题:以绳测井,若将绳三折测之,绳多四尺:若将绳四折测之,绳多一尺.绳长、井深各几何?
这道题大致意思是:用绳子测量水井深度,如果将绳子折成三等份,那么每等份井外余绳四尺:如果将绳子折成四等份,那么每等份井外余绳一尺.问绳长和井深各多少尺?若设井深为x尺,则求解井深的方程正确的是( )
A.3(x+4)=4(x+1)B.3x+4=4x+1
C.![]() x+4=
x+4=![]() x+1D.
x+1D.![]() x﹣4=
x﹣4=![]() x﹣1
x﹣1
查看答案和解析>>
科目: 来源: 题型:
【题目】“十一”期间沈阳世博园(10月1日)的进园人数为![]() 万人,以后的6天里每天的进园人数变化如下表(正数表示比前一天多的人数负数表示比前一天少的人数,单位:万人)
万人,以后的6天里每天的进园人数变化如下表(正数表示比前一天多的人数负数表示比前一天少的人数,单位:万人)
日期 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化 |
|
|
|
|
|
|
(1)10月2日的进园人数是多少?
(2)10月1日-10月7日这7天内的进园人数最多的是哪天?最少的是哪天?它们相差多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com