（1）求∠AEC的度数；

（2）若将图1中的线段AD沿MN向右平移到A1D1如图2所示位置，此时A1E平分∠AA1D1，CE平分∠ACD1，A1E与CE相交于E，∠PAC＝50°，∠A1D1C＝30°，求∠A1EC的度数．

（3）若将图1中的线段AD沿MN向左平移到A1D1如图3所示位置，其他条件与（2）相同，求此时∠A1EC的度数．

（1）填写下表：

（2）照这样的规律搭下去，摆个这样的图形需要 个小圆.

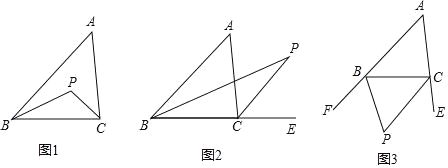
（1）如图1，在△ABC中，BP平分∠ABC，CP平分∠ACB．求证：∠P＝90°+∠A．

（2）如图2，在△ABC中，BP平分∠ABC，CP平分外角∠ACE．猜想∠P和∠A有何数量关系，并证明你的结论．

（3）如图3，BP平分∠CBF，CP平分∠BCE．猜想∠P和∠A有何数量关系，请直接写出结论．

A. 36° B. 40° C. 45° D. 50°

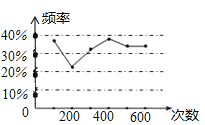
A．从一个装有2个白球和1个红球的袋子中任取两球，取到两个白球的概率

B．任意写一个正整数，它能被 2 整除的概率

C．抛一枚硬币，连续两次出现正面的概率

D．掷一枚正六面体的骰子，出现 1 点的概率

【题目】如图，在数轴上，点表示1，现将点沿轴做如下移动，第一次点向左移动3个单位长度到达点，第二次将点向右移动6个单位长度到达点，第三次将点向左移动9个单位长度到达点，按照这种移动规律移动下去，第次移动到点，如果点与原点的距离不小于20，那么的最小值是__________．

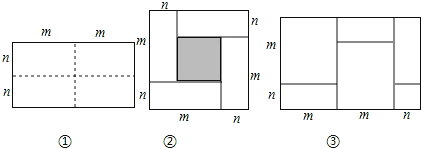
（1）按要求填空：

①你认为图②中的阴影部分的正方形的边长等于　 　；

②请用两种不同的方法表示图②中阴影部分的面积：

方法1：　 　

方法2：　 　

③观察图②，请写出代数式（m+n）2，（m﹣n）2，mn这三个代数式之间的等量关系：　 　；

（2）根据（1）题中的等量关系，解决如下问题：若|m+n﹣6|+|mn﹣4|=0，求（m﹣n）2的值．

（3）实际上有许多代数恒等式可以用图形的面积来表示，如图③，它表示了　 　．

【题目】如图，公共汽车行驶在笔直的公路上，这条路上有四个站点，每相邻两站之间的距离为千米，从站开往站的车称为上行车，从站开往站的车称为下行车．第一班上行车、下行车分别从站、站同时发车，相向而行，且以后上行车、下行车每隔分钟分别在站同时发一班车，乘客只能到站点上、下车(上、下车的时间忽略不计)，上行车、 下行车的速度均为千米/小时．

第一班上行车到站、第一班下行车到站分别用时多少？

第一班上行车与第一班下行车发车后多少小时相距千米？

一乘客在两站之间的处，刚好遇到上行车，千米，他从处以千米/小时的速度步行到站乘下行车前往站办事．

①若千米，乘客从处到达站的时间最少要几分钟？

②若千米，乘客从处到达站的时间最少要几分钟？

【题目】如图，阶梯图的每个台阶上都标着一个数， 从下到上的第个至第个台阶上依次标着，且任意相邻四个台阶上的数的和都相等．

求前个台阶上的数的和；

求第个台阶上的数x的值；

从下到上前为奇数)个台阶上的数的和能否为？若能，求出的值；若不能，请说明理由．