科目： 来源： 题型：
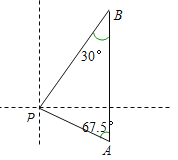
【题目】马航MH370 客机“失联”，我国“海巡01号”前往搜寻。如图某天上午9时,“海巡01号” 轮船位于A处，观测到某小岛P位于轮船的北偏西67.5°，轮船以21海里/时的速度向正北方向行驶，下午2时该船到达B处，这时观测到小岛P位于该船的南偏西30°方向，求此时轮船所处位置B与小岛P的距离？（精确到0.1）
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，从热气球C处测得地面A、B两点的俯角分别为30°、45°，如果此时热气球C处的高度为200米，点A、B、C在同一直线上，则AB两点间的距离是________米（结果保留根号）．
查看答案和解析>>
科目： 来源： 题型：
【题目】某地下车库出口处安装了“两段式栏杆”，点A是栏杆转动的支点，点E是栏杆两段的联结点．当车辆经过时，栏杆AEF最多只能升起到如图所示的位置，其中AB⊥BC，EF∥BC，∠AEF=135°，AB=AE=1.3米，那么适合该地下车库的车辆限高标志牌为（栏杆宽度忽略不计．参考数据：
≈1.4）（ )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，某水渠的横断面是等腰梯形，已知其斜坡AD的坡度为1：1.2，斜坡BC的坡度为1：0.8，现测得放水前的水面宽EF为3.8米，当水闸放水后，水渠内水面宽GH为6米．则放水后水面上升的高度是（ ）米．
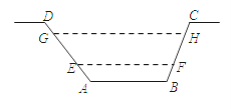
A. 1.2 B. 1.1 C. 0.8 D. 2.2
查看答案和解析>>
科目： 来源： 题型：
【题目】已知：
，OE平分
，点A、B、C分别是射线OM、OE、ON上的动点
、B、C不与点O重合
，连接AC交射线OE于点
设
．
如图1，若
，则
的度数是______；
当
时，
______；当
时，______．
如图2，若
，则是否存在这样的x的值，使得
中有两个相等的角？若存在，求出x的值；若不存在，说明理由．
查看答案和解析>>
科目： 来源： 题型：
【题目】阅读材料：
我们可以用配方法求一个二次三项式的最大值或最小值，例如：求代数式
的最小值.方法如下：
解：
∵
，得
，
∴代数式的最小值是4.
请根据上述材料，解决下列问题：
(1)求代数式
的最小值.
(2)用配方法求代数式
的最值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
