
科目: 来源: 题型:
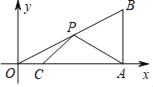
【题目】如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,顶点B的坐标为(3,![]() ),点C的坐标为(1,0),且∠B=60°,点P为斜边OB上的一个动点,则PA+PC的最小值为_____.
),点C的坐标为(1,0),且∠B=60°,点P为斜边OB上的一个动点,则PA+PC的最小值为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图(1),已知:在等腰直角三角形![]() 中,
中,![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() 直线
直线![]() ,
,![]() 直线
直线![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() .则
.则![]() 、
、![]() 和
和![]() 之间的数量关系是: .
之间的数量关系是: .
(2)如图(2),将(1)中的条件改为:在等腰三角形![]() 中,
中,![]() 、
、![]() 、
、![]() 三点都在直线
三点都在直线![]() 上,且
上,且![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论
为任意锐角或钝角.请问结论![]() 是否成立?如成立,请你给出证明;若不成立,请说明理由.
是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),![]() 、
、![]() 是直线
是直线![]() 上的两动点(
上的两动点(![]() 、
、![]() 、
、![]() 三点互不重合),点
三点互不重合),点![]() 为
为![]() 平分线上的一点,且
平分线上的一点,且![]() 和
和![]() 均为等边三角形,连接
均为等边三角形,连接![]() 、
、![]() ,若
,若![]() ,求证:
,求证:![]() .
.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 和
和![]() 都是等腰三角形,
都是等腰三角形,![]() ,
,![]() ,
,![]() .
.
(初步感知)(1)特殊情形:如图①,若点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,则
上,则![]() __________
__________![]() .(填>、<或=)
.(填>、<或=)

(2)发现证明:如图②,将图①中的![]() 绕点
绕点![]() 旋转,当点
旋转,当点![]() 在
在![]() 外部,点
外部,点![]() 在
在![]() 内部时,求证:
内部时,求证:![]() .
.

(深入研究)(3)如图③,![]() 和
和![]() 都是等边三角形,点
都是等边三角形,点![]() ,
,![]() ,
,![]() 在同一条直线上,则
在同一条直线上,则![]() 的度数为__________;线段
的度数为__________;线段![]() ,
,![]() 之间的数量关系为__________.
之间的数量关系为__________.

(4)如图④,![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() ,点
,点![]() 、
、![]() 、
、![]() 在同一直线上,
在同一直线上,![]() 为
为![]() 中
中![]() 边上的高,则
边上的高,则![]() 的度数为__________;线段
的度数为__________;线段![]() ,
,![]() ,
,![]() 之间的数量关系为__________.
之间的数量关系为__________.

(拓展提升)(5)如图⑤,![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转,连结
逆时针旋转,连结![]() 、
、![]() .当
.当![]() ,
,![]() 时,在旋转过程中,
时,在旋转过程中,![]() 与
与![]() 的面积和的最大值为__________.
的面积和的最大值为__________.

查看答案和解析>>
科目: 来源: 题型:
【题目】某篮球运动员去年共参加40场比赛,其中3分球的命中率为0.25,平均每场有12次3分球未投中.
(1)该运动员去年的比赛中共投中多少个3分球?
(2)在其中的一场比赛中,该运动员3分球共出手20次,小亮说,该运动员这场比赛中一定投中了5个3分球,你认为小亮的说法正确吗?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明站在池塘边的![]() 点处,池塘的对面(小明的正北方向)
点处,池塘的对面(小明的正北方向)![]() 处有一棵小树,他想知道这棵树距离他有多远,于是他向正东方向走了12步到达电线杆
处有一棵小树,他想知道这棵树距离他有多远,于是他向正东方向走了12步到达电线杆![]() 旁,接着再往前走了12步,到达
旁,接着再往前走了12步,到达![]() 处,然后他改向正南方向继续行走,当小明看到电线杆
处,然后他改向正南方向继续行走,当小明看到电线杆![]() 、小树
、小树![]() 与自己现处的位置
与自己现处的位置![]() 在一条直线上时,他共走了60步.
在一条直线上时,他共走了60步.
(1)根据题意,画出示意图(写出作图步骤);
(2)如果小明一步大约40 ![]() ,估算出小明在点
,估算出小明在点![]() 处时小树与他的距离为多少米,并说明理由.
处时小树与他的距离为多少米,并说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】儿童节期间,某公园游戏场举行一场活动.有一种游戏的规则是:在一个装有8个红球和若干白球(每个球除颜色外,其他都相同)的袋中,随机摸一个球,摸到一个红球就得到一个海宝玩具.已知参加这种游戏的儿童有40 000人,公园游戏场发放海宝玩具8 000个.
(1)求参加此次活动得到海宝玩具的频率?
(2)请你估计袋中白球的数量接近多少个?
查看答案和解析>>
科目: 来源: 题型:
【题目】直角三角形![]() 中,
中,![]() ,直线
,直线![]() 过点
过点![]() .
.
(1)当![]() 时,如图①,分别过点
时,如图①,分别过点![]() 、
、![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() .求证:
.求证:![]() .
.
(2)当![]() ,
,![]() 时,如图②,点
时,如图②,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,连接
对称,连接![]() 、
、![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿![]() 边向终点
边向终点![]() 运动,同时动点
运动,同时动点![]() 从点
从点![]() 出发,以每秒3个单位的速度沿
出发,以每秒3个单位的速度沿![]() 向终点
向终点![]() 运动,点
运动,点![]() 、
、![]() 到达相应的终点时停止运动,过点
到达相应的终点时停止运动,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,设运动时间为
,设运动时间为![]() 秒.
秒.
①用含![]() 的代数式表示
的代数式表示![]() .
.
②直接写出当![]() 与
与![]() 全等时
全等时![]() 的值.
的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】下列实验中,概率最大的是【 】
A. 抛掷一枚质地均匀的硬币,出现正面;
B. 抛掷一枚质地均匀的正方体骰子(六个面分别刻有数字1到6),掷出的点数为奇数;
C. 在一副洗匀的扑克(背面朝上)中任取一张,恰好为方块;
D. 三张同样的纸片,分别写有数字2,3,4,和匀后背面朝上,任取一张恰好为偶数
查看答案和解析>>
科目: 来源: 题型:
【题目】小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:营业员![]() :月销售件数100件,月总收入2400元;营业员
:月销售件数100件,月总收入2400元;营业员![]() :月销售件数150件,月总收入2700元;假设营业员的月基本工资为
:月销售件数150件,月总收入2700元;假设营业员的月基本工资为![]() 元,销售每件服装奖励
元,销售每件服装奖励![]() 元.
元.
(1)求![]() 、
、![]() 的值.
的值.
(2)若某营业员的月总收入不低于3200元,则她当月至少要卖出服装多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com