
科目: 来源: 题型:
【题目】某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动,每位同学必须且只能选择一项球类运动,对该校学生随机抽取![]() 进行调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
进行调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
运动项目 | 频数(人数) |
羽毛球 | 30 |
篮球 |
|
乒乓球 | 36 |
排球 |
|
足球 | 12 |

请根据以上图表信息解答下列问题:
(1)频数分布表中的![]() ,
,![]() ;
;
(2)在扇形统计图中,“排球”所在的扇形的圆心角为 度;
(3)全校有多少名学生选择参加乒乓球运动?
查看答案和解析>>
科目: 来源: 题型:
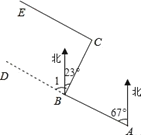
【题目】如图,某工程队从A点出发,沿北偏西67°方向修一条公路AD,在BD路段出现塌陷区,就改变方向,由B点沿北偏东23°的方向继续修建BC段,到达C点又改变方向,从C点继续修建CE段,∠ECB应为多少度,可使所修路段CE∥AB?试说明理由.此时CE与BC有怎样的位置关系?
以下是小刚不完整的解答,请帮他补充完整.
解:由已知平行,得∠1=∠A=67°(两直线平行, )
∴∠CBD=23°+67°= °,
当∠ECB+∠CBD= °时,
可得CE∥AB.( )
所以∠ECB= °
此时CE⊥BC.( )
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).

(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值.
查看答案和解析>>
科目: 来源: 题型:
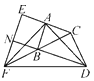
【题目】如图,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB=CD.延长CA至点E,使AE=AC;延长CB至点F,使BF=BC.连接AD,AF,DF,EF.延长DB交EF于点N.
(1)求证:AD=AF;
(2)求证:BD=EF;
(3)试判断四边形ABNE的形状,并说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点
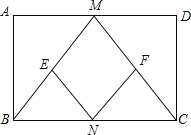
(1)求证:△ABM≌△DCM
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB= _时,四边形MENF是正方形(只写结论,不需证明)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).
(1)在图中作出△ABC关于y轴对称的△A1B1C1;
(2)写出点C1的坐标(直接写答案):C1 ;
(3)△A1B1C1的面积为 ;
(4)在y轴上画出点P,使PB+PC最小.

查看答案和解析>>
科目: 来源: 题型:
【题目】(2016新疆)如图,ABCD中,AB=2,AD=1,∠ADC=60°,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若点P时直线l上的一个动点,请计算PD′+PB的最小值.

查看答案和解析>>
科目: 来源: 题型:
【题目】为提高学生的阅读能力,市教研室开展了“教材+阅读”工程活动,某校进行了“我喜爱的一本书”征文比赛,为奖励在比赛中表现优异的同学,学校准备从书店一次性购买若干本《中华散文百年精华》和《傅雷家书》,购买1本《中华散文百年精华》和1本《傅雷家书》共需159元;《中华散文百年精华》单价是《傅雷家书》单价的2倍少9元.
(1)求《中华散文百年精华》和《傅雷家书》的单价各是多少元?
(2)根据学校实际情况,需一次性购买《中华散文百年精华》和《傅雷家书》共20本,但要求购买的总费用不超过1550元,学校最多可以购买多少本《中华散文百年精华》?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:
①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF=![]() S△ABC;④EF=AP.上述结论始终正确的有( )
S△ABC;④EF=AP.上述结论始终正确的有( )
②③

A.①②③④B.①②③C.①③④D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com