
科目: 来源: 题型:
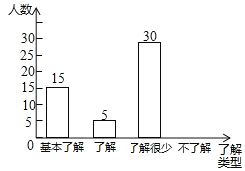
【题目】“校园安全”受到全社会的广泛关注,“高远”中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如下尚不完整的条形统计图,且知在抽样调查中“了解很少”的同学占抽样调查人数的![]() ,请你根据提供的信息解答下列问题:
,请你根据提供的信息解答下列问题:
![]() 接受问卷调查的学生共有多少名?
接受问卷调查的学生共有多少名?
![]() 请补全条形统计图;
请补全条形统计图;
![]() 若“高远”中学共有1800名学生,请你估计该校学生对校园知识“基本了解”的有多少名?
若“高远”中学共有1800名学生,请你估计该校学生对校园知识“基本了解”的有多少名?
查看答案和解析>>
科目: 来源: 题型:
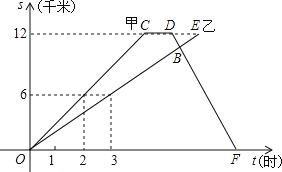
【题目】甲、乙两名同学进行登山比赛,甲同学和乙同学沿相同的路线同时在早8:00从山脚出发前往山顶,甲同学到达山顶后休息1小时,沿原路以每小时6千米的速度下山,在这一过程中,各自行进的路程随所用时间变化的图象如图所示,根据提供信息得出以下四个结论:
![]() 甲同学从山脚到达山顶的路程为12千米;
甲同学从山脚到达山顶的路程为12千米;
![]() 乙同学登山共用4小时;
乙同学登山共用4小时;
![]() 甲同学在14:00返回山脚;
甲同学在14:00返回山脚;
![]() 甲同学返回与乙同学相遇时,乙同学距登到山顶还有
甲同学返回与乙同学相遇时,乙同学距登到山顶还有![]() 千米的路程.
千米的路程.
以上四个结论正确的有![]()
![]() 个
个
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图所示,直线MN∥GH,另一直线交GH于A,交MN于B,且∠MBA=80°,点C为直线GH上一动点,点D为直线MN上一动点,且∠GCD=50°.

(1)如图1,当点C在点A右边且点D在点B左边时,∠DBA的平分线交∠DCA的平分线于点P,求∠BPC的度数;
(2)如图2,当点C在点A右边且点D在点B右边时,∠DBA的平分线交∠DCA的平分线于点P,求∠BPC的度数;
(3)当点C在点A左边且点D在点B左边时,∠DBA的平分线交∠DCA的平分线所在直线交于点P,请直接写出∠BPC的度数,不说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明家距离学校8千米,今天早晨,小明骑车上学图中,自行车出现故障,恰好路边有便民服务点,几分钟后车修好了,他以更快的速度匀速骑车到校.我们根据小明的这段经历画了一幅图象(如图),该图描绘了小明行驶的路程(千米)与他所用的时间(分钟)之间的关系.请根据图象,解答下列问题:

(1)小明行了多少千米时,自行车出现故障?修车用了几分钟?
(2)小明从早晨出发直到到达学校共用了多少分钟?
(3)小明修车前、后的行驶速度分别是多少?
(4)如果自行车未出现故障,小明一直用修车前的速度行驶,那么他比实际情况早到或晚到多少分钟?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目: 来源: 题型:
【题目】一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg.且不高于180元/kg,经销一段时间后得到如下数据:
销售单价x(元/kg) | 120 | 130 | … | 180 |
每天销量y(kg) | 100 | 95 | … | 70 |
设y与x的关系是我们所学过的某一种函数关系.
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.

(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,在平面直角坐标系中,A(m,0)、B(0,n),m、n满足(m-n)2+|m-![]() |=0.C为AB的中点,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
|=0.C为AB的中点,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.

(1)求∠OAB的度数;
(2)设AB=4,当点P运动时,PE的值是否变化?若变化,说明理由;若不变,请求PE的值;
(3)设AB=4,若∠OPD=45°,求点D的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.

(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com