
科目: 来源: 题型:
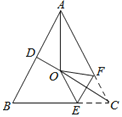
【题目】如图,在等腰![]() ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
A. 60° B. 55° C. 50° D. 45°
查看答案和解析>>
科目: 来源: 题型:
【题目】探索与发现
探索:如图,在直角坐标系中,正方形ABCO的点B坐标(4,4),点A、C分别在y轴、x轴上,对角线AC上一动点E,连接BE,过E作DE⊥BE交OC于点D.

(1)证明:BE=DE.
小明给出的思路为:过E作y轴的平行线交AB、x轴于点F、H.请完善小明的证明过程.
(2)若点D坐标为(3,0),则点E坐标为 .
若点D坐标为(a,0),则点E坐标为 .
发现:在直角坐标系中,点B坐标(5,3),点D坐标(3,0),找一点E,使得△BDE为等腰直角三角形,直接写出点E坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数![]() 的部分图象如图,图象过点(﹣1,0),对称轴为直线
的部分图象如图,图象过点(﹣1,0),对称轴为直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时, ![]() 随
随![]() 的增大而增大.其中正确的结论有( )
的增大而增大.其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】(阅读)如图1,等边△ABC中,P是AC边上一点,Q是CB延长线上一点,若AP=BQ.则过P作PF∥BC交AB于F,可证△APF是等边三角形,再证△PDF≌QDB可得D是FB的中点.请写出证明过程.
(运用)如图2,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A,C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.

(1)当∠BQD=30°时,求AP的长;
(2)在运动过程中线段ED的长是否发生变化?如果不变,直接写出线段ED的长;如果发生改变,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,Rt△AOB中,∠AOB=90°,AO=3BO,OB在x轴上,将Rt△AOB绕点O顺时针旋转至△RtA'OB',其中点B'落在反比例函数y=﹣![]() 的图象上,OA'交反比例函数y=
的图象上,OA'交反比例函数y=![]() 的图象于点C,且OC=2CA',则k的值为( )
的图象于点C,且OC=2CA',则k的值为( )

A. 4 B. ![]() C. 8 D. 7
C. 8 D. 7
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知AB=12cm,CA⊥AB于点A,DB⊥AB于点B,且AC=4cm,点P从点B向点A运动,每秒钟走1cm,点Q从点B向点D运动,每秒钟走2cm,两点同时出发,运动几秒钟后,△CPA与△PQB全等?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,(图1,图2),四边形ABCD是边长为4的正方形,点E在线段BC上,∠AEF=90°,且EF交正方形外角平分线CP于点F,交BC的延长线于点N, FN⊥BC.
(1)若点E是BC的中点(如图1),AE与EF相等吗?
(2)点E在BC间运动时(如图2),设BE=x,△ECF的面积为y。
①求y与x的函数关系式;
②当x取何值时,y有最大值,并求出这个最大值.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线y=x+3与坐标轴分别交于A,B两点,抛物线y=ax2+bx-3a经过点A,B,顶点为C,连接CB并延长交x轴于点E,点D与点B关于抛物线的对称轴MN对称.

(1)求抛物线的解析式及顶点C的坐标;
(2)求证:四边形ABCD是直角梯形.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了对学生进行爱国主义教育,某校组织学生去看演出,有甲乙两种票,已知甲乙两种票的单价比为4:3,单价和为42元.
(1)甲乙两种票的单价分别是多少元?
(2)学校计划拿出不超过750元的资金,让七年级一班的36名学生首先观看,且规定购买甲种票必须多于15张,有哪几种购买方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com