
科目: 来源: 题型:
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )

A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
科目: 来源: 题型:
【题目】某校![]() 名学生参加植树活动,要求每人植
名学生参加植树活动,要求每人植![]() 棵,活动结束后随机抽查了
棵,活动结束后随机抽查了![]() 名学生每人的植树量,并分为四种类型,
名学生每人的植树量,并分为四种类型,![]() :
:![]() 棵;
棵;![]() ;
;![]() 棵;
棵;![]() :
:![]() 棵,
棵,![]() :
:![]() 棵。将各类的人绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误。
棵。将各类的人绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误。

回答下列问题:
(1)写出条形图中存在的错误,并说明理由.
(2)写出这![]() 名学生每人植树量的众数、中位数.
名学生每人植树量的众数、中位数.
(3)在求这![]() 名学生每人植树量的平均数.
名学生每人植树量的平均数.
(4)估计这![]() 名学生共植树多少棵.
名学生共植树多少棵.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知正方形ABCD的边长为10cm,点E在边AB上,且AE=4cm,

(1)如果点P在线段BC上以2cm/s的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.
①若点Q的运动速度与点P的运动速度相等,经过2秒后,△BPE与△CQP是否全等?请说明理由.
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为________cm/s时,在某一时刻也能够使△BPE与△CQP全等.
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿正方形ABCD的四条边运动.求经过多少秒后,点P与点Q第一次相遇,并写出第一次相遇点在何处?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,要测量河流![]() 的长,因为无法测河流附近的点
的长,因为无法测河流附近的点![]() ,可以在
,可以在![]() 线外任取一点
线外任取一点![]() ,在
,在![]() 的延长线上任取一点
的延长线上任取一点![]() ,连结
,连结![]() 和
和![]() ,并且延长
,并且延长![]() 到点
到点![]() ,使
,使![]() ;延长
;延长![]() 到点
到点![]() ,使
,使![]() 连结
连结![]() ,并延长
,并延长![]() 到点
到点![]() ,使点
,使点![]() ,
,![]() ,
,![]() 在同一直线上.证明:测量出线段
在同一直线上.证明:测量出线段![]() 的长就是河流
的长就是河流![]() 的长.
的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,二次函数图象的顶点坐标为C(1,﹣2),直线y=kx+m的图象与该二次函数的图象交于A、B两点,其中A点坐标为(3,0),B点在y轴上.点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这个二次函数的图象交于点E.
(1)求这个二次函数的解析式;
(2)设点P的横坐标为x,求线段PE的长(用含x 的代数式表示);
(3)点D为直线AB与这个二次函数图象对称轴的交点,若以点P、E、D为顶点的三角形与△AOB相似,请求出P点的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
(1)求证:EG=CG且EG⊥CG;
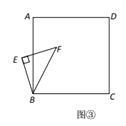
(2)将图①中△BEF绕B点逆时针旋转45,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?


查看答案和解析>>
科目: 来源: 题型:
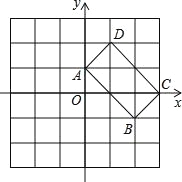
【题目】如图,在 6×6 的网格中,四边形 ABCD 的顶点都在格点上,每个格子都是边长为 1 的正方形,建立如图所示的平面直角坐标系.
(1)画出四边形 ABCD 关于 y 轴对称和四边形 A′B′C′D′(点 A、B、C、D的对称点分别是点 A′B′C′D′.
(2)求 A、B′、B、C 四点组成和四边形的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,分别过B,C向经过点A的直线EF作垂线,垂足为E,F.

(1)如图1,当EF与斜边BC不相交时,请证明EF=BE+CF;
(2)如图2,当EF与斜边BC相交时,其他条件不变,写出EF、BE、CF之间的数量关系,并说明理由;
(3)如图3,猜想EF、BE、CF之间又存在怎样的数量关系,写出猜想,不必说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据消费者需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的![]() ,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案?
②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com