
科目: 来源: 题型:
【题目】某校九年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题选择一个,九年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.

(1)求共抽取了多少名学生的征文;
(2)将上面的条形统计图补充完整;
(3)在扇形统计图中,选择“爱国”主题所对应的圆心角是多少;
(4)如果该校九年级共有1200名学生,请估计选择以“友善”为主题的九年级学生有多少名.
查看答案和解析>>
科目: 来源: 题型:
【题目】下表是某校“河南省汉子听写大赛初赛”冠军组成员的年龄分布
年龄/岁 | 12 | 13 | 14 | 15 |
人数 | 5 | 15 | x | 12﹣x |
对于不同的x,下列关于年龄的统计量不会发生改变的是( )
A. 平均数、中位数 B. 平均数、方差 C. 众数、中位数 D. 中位数、方差
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读以下材料:
对数的创始人是苏格兰数学家纳皮尔(J.Nplcr,1550-1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evlcr,1707-1783年)才发现指数与对数之间的联系.
对数的定义:一般地,若ax=N(a>0,a≠1),那么x叫做以a为底N的对数,记作:x=logaN.比如指数式24=16可以转化为4=log216,对数式2=log525可以转化为52=25.
我们根据对数的定义可得到对数的一个性质:loga(MN)=logaM+logaN(a>0,a≠1,M>0,N>0);理由如下:
设logaM=m,logaN=n,则M=am,N=an
∴MN=aman=am+n,由对数的定义得m+n=loga(MN)
又∵m+n=logaM+logaN
∴loga(MN)=logaM+logaN
解决以下问题:
(1)将指数43=64转化为对数式: .
(2)仿照上面的材料,试证明:![]() =
=![]() —
—![]() (a>0,a
(a>0,a![]() l,M>0,N>0).
l,M>0,N>0).
(3) 拓展运用:计算log32+log36-log34=____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知A(﹣2,0),B(4,0),抛物线y=ax2+bx﹣1过A、B两点,并与过A点的直线y=﹣![]() x﹣1交于点C.
x﹣1交于点C.
(1)求抛物线解析式及对称轴;
(2)在抛物线的对称轴上是否存在一点P,使四边形ACPO的周长最小?若存在,求出点P的坐标,若不存在,请说明理由;
(3)点M为y轴右侧抛物线上一点,过点M作直线AC的垂线,垂足为N.问:是否存在这样的点N,使以点M、N、C为顶点的三角形与△AOC相似,若存在,求出点N的坐标,若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为![]() 的大正方形,两块是边长都为
的大正方形,两块是边长都为![]() 的小正方形,五块是长为
的小正方形,五块是长为![]() 、宽为
、宽为![]() 的全等小矩形,且
的全等小矩形,且![]() >
> ![]() .(以上长度单位:cm)
.(以上长度单位:cm)
(1)观察图形,可以发现代数式![]() 可以因式分解为 ;
可以因式分解为 ;
(2)若每块小矩形的面积为10![]() ,四个正方形的面积和为58
,四个正方形的面积和为58![]() ,试求图中所有裁剪线(虚线部分)长之和.
,试求图中所有裁剪线(虚线部分)长之和.

查看答案和解析>>
科目: 来源: 题型:
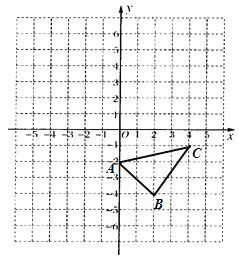
【题目】已知:如图,在平面直角坐标系中.
(1)作出△ABC关于![]() 轴对称的
轴对称的![]() ,并写出
,并写出![]() 三个顶点的坐标:
三个顶点的坐标: ![]() ( ),
( ),![]() ( ),
( ),![]() ( );
( );
(2)直接写出△ABC的面积为 ;
(3)在![]() 轴上画点P,使PA+PC最小.
轴上画点P,使PA+PC最小.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将矩形ABCD绕点A按逆时针方向旋转,得到矩形AEFG,E点正好落在边CD上,连接BE,BG,且BG交AE于P.
(1)求证:∠CBE=![]() ∠BAE;
∠BAE;
(2)求证:PG=PB;
(3)若AB=![]() ,BC=3,求出BG的长.
,BC=3,求出BG的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】某商城销售A,B两种自行车.A型自行车售价为2 100元/辆,B型自行车售价为1 750元/辆,每辆A型自行车的进价比每辆B型自行车的进价多400元,商城用80 000元购进A型自行车的数量与用64 000元购进B型自行车的数量相等.
(1)求每辆A,B两种自行车的进价分别是多少?
(2)现在商城准备一次购进这两种自行车共100辆,设购进A型自行车m辆,这100辆自行车的销售总利润为y元,要求购进B型自行车数量不超过A型自行车数量的2倍,总利润不低于13 000元,求获利最大的方案以及最大利润.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC,点D在斜边AB上,且AD=AC,过点B作BE⊥CD,交直线CD于点E.
(1)求∠BCD的度数;
(2)作AF⊥CD于点F,求证:△AFD≌△CEB;
(3)请直接写出CD与BE的数量关系(不需要证明).

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,等边△A1C1C2的周长为1,作C1D1⊥A1C2于D1,在C1C2的延长线上取点C3,使D1C3=D1C1,连接D1C3,以C2C3为边作等边△A2C2C3;作C2D2⊥A2C3于D2,在C2C3的延长线上取点C4,使D2C4=D2C2,连接D2C4,以C3C4为边作等边△A3C3C4;…且点A1,A2,A3,…都在直线C1C2同侧,如此下去,则△A1C1C2,△A2C2C3,△A3C3C4,…,△AnnCn+1的周长和为_____.(n≥2,且n为整数)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com