
科目: 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,点B、C、E三点在同一条直线上, CD平分∠ACE, DB=DA,DM⊥BE于M.
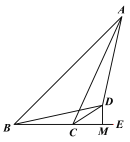
(1)求证:AC=BM+CM;
(2)若AC=2,BC=1,求CM的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】定义:如图1,在△ABC和△ADE中,AB=AC=AD=AE,当∠BAC+∠DAE=180° 时,我们称△ABC与△DAE互为“顶补等腰三角形”,△ABC的边BC上的高线AM叫做△ADE的“顶心距”,点A叫做“旋补中心”.

(1)特例感知:在图2,图3中,△ABC与△DAE互为“顶补等腰三角形”,AM是“顶心距”。
①如图2,当∠BAC=90°时,AM与DE之间的数量关系为AM= DE;
②如图3,当∠BAC=120°,ED=6时,AM的长为 。
(2)猜想论证:
在图1中,当∠BAC为任意角时,猜想AM与DE之间的数量关系,并给予证明。

(3)拓展应用
如图4,在四边形ABCD中,AD=AB,CD=BC,∠B=90°,∠A=60°,CA=![]() ,在四边ABCD的内部找到点P,使得△PAD与△PBC互为“顶补等腰三角形”。并回答下列问题。
,在四边ABCD的内部找到点P,使得△PAD与△PBC互为“顶补等腰三角形”。并回答下列问题。
①请在图中标出点P的位置,并描述出该点的位置为 ;
②直接写出△PBC的“顶心距”的长为 。

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABE中,∠BAE=105°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )

A. 45°B. 60°C. 50°D. 55°
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD 中,AB=AD,点B关于AC的对称点B′恰好落在CD上,若∠BAD=![]() ,则∠ACB的度数为( )
,则∠ACB的度数为( )

A. ![]() α B. 90°-
α B. 90°-![]() α C. 45° D. α-45°
α C. 45° D. α-45°
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,AB=4,BC=3,点D从B点出发,沿射线CB方向以每秒3个单位长度的速度运动,射线MP⊥射线CB,且BM=10,点Q从M点出发,沿射线MQ方向以每秒a个单位长度的速度运动,已知D、Q两点同时出发,运动时间为t秒.
(1)当t=2时,△DMQ是等腰三角形,求a的值.
(2)求t为何值时,△DCA为等腰三角形.
(3)是否存在a,使得△DMQ与△ABC全等,若存在,请直接写出a的值,若不存在,请说明理由.
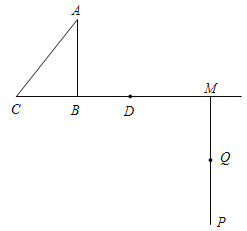
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D,E,F分别在边BC,AC,AB上,且BD=CE,DC=BF,连结DE,EF,DF,∠1=60°
(1)求证:△BDF≌△CED.
(2)判断△ABC的形状,并说明理由.
(3)若BC=10,当BD= 时,DF⊥BC.(只需写出答案,不需写出过程)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,CE平分∠DCB交AB于点E.
(1)求证:∠AEC=∠ACE;
(2)若∠AEC=2∠B,AD=2,求AB的长.
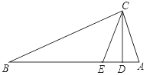
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com